KuiperDatawhale
本次课程为KuiperInfer的子项目(学习项目)。
完整推理框架项目地址:https://github.com/zjhellofss/kuiperInfer
B站课程地址:https://www.bilibili.com/video/BV118411f7yM/?spm_id_from=333.788&vd_source=841bd3506b40b195573d34fef4c5bdf7
本人学习项目地址:https://github.com/caixiongjiang/HPC
一:环境搭建
推理框架要完成的功能
- 对已经训练完成的神经网络模型文件进行加载
- 根据网络结构和权重参数对输入图像进行预测
- 推理阶段的权重已经固定,不需要后向传播技术
推理框架的模块
Operator:深度学习计算图中的计算节点,包含:
- 存储输入输出的张量
- 计算节点的类型和名称
- 计算节点参数信息(Params:卷积的步长,卷积核的大小等)
- 计算节点的权重信息(attributes:存储weights和bias)
Graph:多个Operator串联得到的有向无环图,规定了各个节点(Operator)执行的流程和顺序。Layer:计算节点运算具体的执行者,Layer类先读入输入张量中的数据,然后对输入张量进行计算,不同的算子中Layer的计算过程会不一致!Tensor:用于存放多维数据的数据结构,方便数据在计算节点之间传递,同时该结构也封装矩阵乘、点积等与矩阵相关的基本操作。
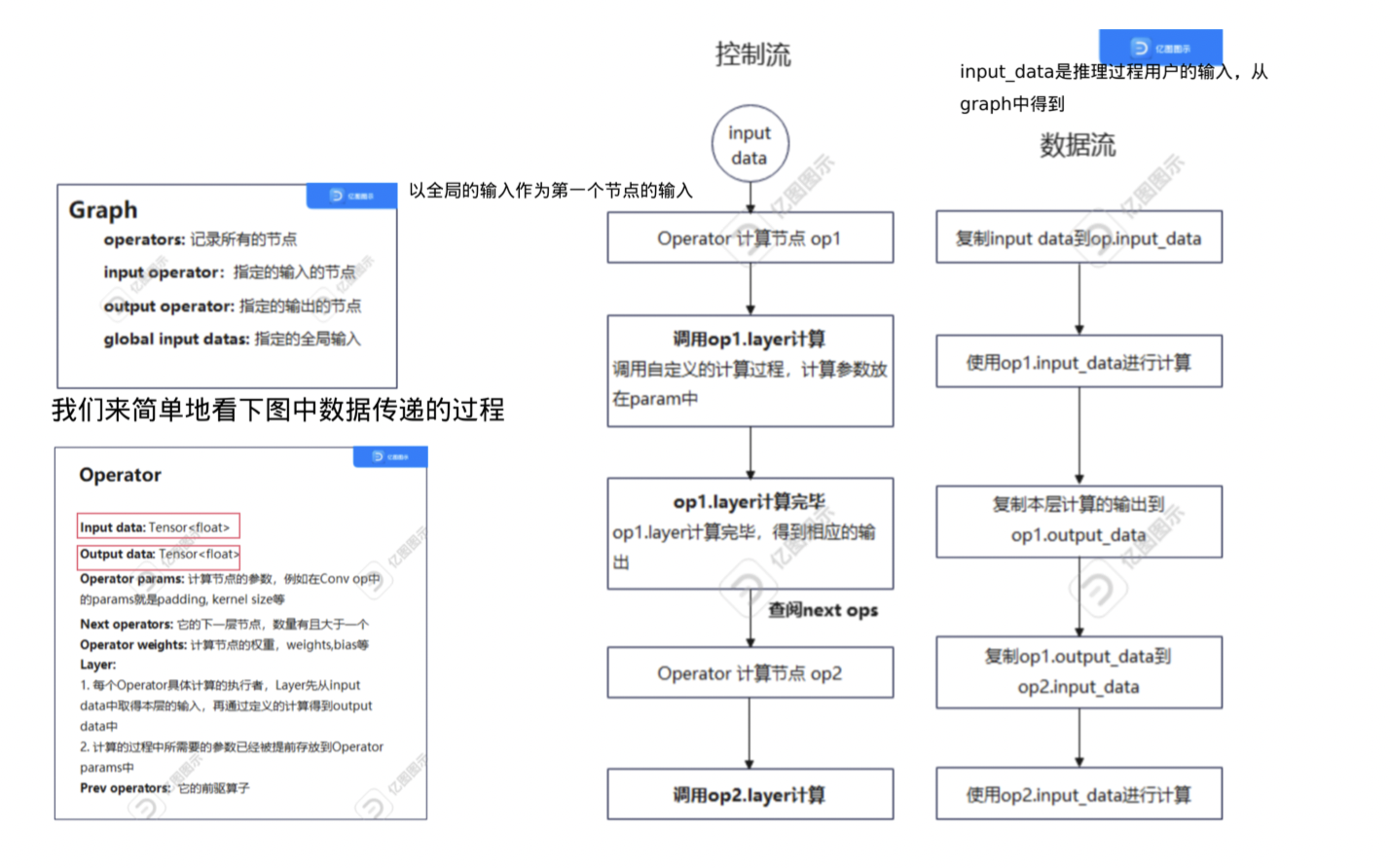
使用的模块
作业:完成测试用例
目的是了解Armadillo数学库的基本用法。
二:张量的设计与实现
张量类的设计
这里在arma::fmat和arma::fcube的基础上进行开发,f代表float,fcube可以看做是fmat的堆叠而成的结构。
与Pytorch中的矩阵存储不同的是,fmat是列主序的,需要进行区分。
张量类的方法
- 创建张量以及返回张量的维度信息:主要有4个属性,
rows,cols,channels,raw_shapes。
其中创建的方法调用了fcube的创建方法:arma::fcube(rows, cols, channels)。返回维度信息的方法分别是rows(),cols(),channels(),size()。
- 张量的填充方法(Fill):需要注意转置的过程(列主序和行主序的区别)
- 对张量进行变形(Reshape)
- 返回是否为空(empty)
作业为实现Flatten和Padding方法
Flatten:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
void Tensor<float>::Flatten(bool row_major) {
CHECK(!this->data_.empty());
/// Homework1: 请补充代码
const uint32_t total_elems = this->data_.size();
const uint32_t rows = this->rows();
const uint32_t cols = this->cols();
const uint32_t channels = this->data_.n_slices;
std::vector<float> flattened_data(total_elems);
if (row_major) {
// 按行主序取数据, arma::fcube数据中,每个channel内的取值顺序是按列主序的,所以需要改变一下取值顺序
for (uint32_t i = 0; i < channels; ++i) {
auto& channel_data = this->data_.slice(i);
// t()代表转置,&的作用:channel_data.t()` 返回的是一个新的 `arma::fmat` 对象,
// 如果没有使用引用类型的变量来接收它,那么程序就无法操作这个新的对象。
const arma::fmat &channel_data_t = channel_data.t();
std::copy(channel_data_t.begin(), channel_data_t.end(), flattened_data.begin() + i * rows * cols);
}
} else {
/// memptr()属于arma数学库中数据的方法,而begin()是c++中vector的方法,作用是相同的,都是返回第一个元素的地址
// 因为arma的数据本身就是列主序,只要将数据所有拷贝到flatten_data中就好了
std::copy(this->data_.memptr(), this->data_.memptr() + total_elems, flattened_data.begin());
}
// 改变数组的shapes
this->data_.set_size(1, total_elems, 1);
// 将flatten数据拷贝回原来的张量,第三个参数接收的是需要拷贝的起始地址
std::copy(flattened_data.begin(), flattened_data.end(), this->data_.memptr());
this->raw_shapes_ = std::vector<uint32_t>{total_elems};
}
|
Padding:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
void Tensor<float>::Padding(const std::vector<uint32_t>& pads,
float padding_value) {
CHECK(!this->data_.empty());
CHECK_EQ(pads.size(), 4);
// 四周填充的维度
uint32_t pad_rows1 = pads.at(0); // up
uint32_t pad_rows2 = pads.at(1); // bottom
uint32_t pad_cols1 = pads.at(2); // left
uint32_t pad_cols2 = pads.at(3); // right
/// Homework2:请补充代码
const uint32_t channels = this->channels();
const uint32_t rows = this->rows();
const uint32_t cols = this->cols();
const uint32_t new_rows = rows + pad_rows1 + pad_rows2;
const uint32_t new_cols = cols + pad_cols1 + pad_cols2;
auto new_tensor = arma::fcube(new_rows, new_cols, channels);
new_tensor.fill(padding_value);
/// `cols()` 和 `rows()` 方法分别返回数据张量的列数和行数。
/// 这个张量的大小是在创建对象时指定的,一旦创建后就不能再改变大小。
/// 拷贝原来张量中的元素到新的张量中
for (uint32_t i = 0; i < channels; ++i) {
for (uint32_t j = 0; j < cols; ++j) {
for (uint32_t k = 0; k < rows; ++k) {
//计算新的单元位置
uint32_t new_j = j + pad_cols1;
uint32_t new_k = k + pad_rows1;
//拷贝元素
new_tensor.at(new_k, new_j, i) = this->data_.at(k, j, i);
}
}
}
// 将新的张量赋值给 data_ 使用move函数,直接将整个对象拷贝了过来
this->data_ = std::move(new_tensor);
// 我们在创建new_tensor的时候已经定义了cols,rows,channels。 还需要指定类内成员raw_shape()_的值
this->raw_shapes_ = std::vector<uint32_t>{channels, new_rows, new_cols};
}
|
三:计算图的定义
我们使用的PNNX计算图,相对于ONNX,其可以使用模版匹配将子图用大的算子代替许多小算子,Pytorch中的算数表达式会被保留,PNNX有大量的图优化技术,包括了算子融合,常量折叠和消除,公共表达式消除等技术!
PNNX计算图的格式
PNNX主要由图结构(Graph),运算符(Operator)和操作数(Operand)三种结构组成,设计简洁。
Operator类用来表示计算图中的运算符(算子),比如一个模型中的Convolution, Pooling等算子;Operand类用来表示计算图中的操作数,即与一个运算符有关的输入和输出张量;Graph类的成员函数提供了方便的接口用来创建和访问操作符和操作数,以构建和遍历计算图。同时,它也是模型中运算符(算子)和操作数的集合。
Operator结构的组成
在PNNX中,Operator用来表示一个算子,它由以下几个部分组成:
inputs:类型为std::vector<operand>, 表示这个算子在计算过程中所需要的输入操作数operand;outputs:类型为std::vector<operand>, 表示这个算子在计算过程中得到的输出操作数operand;type和name类型均为std::string, 分别表示该运算符号的类型和名称;params, 类型为std::map, 用于存放该运算符的所有参数(例如卷积运算符中的params中将存放stride, padding, kernel size等信息);attrs, 类型为std::map, 用于存放该运算符所需要的具体权重属性(例如卷积运算符中的attrs中就存放着卷积的权重和偏移量,通常是一个float32数组)。
Operand的结构组成
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Operand
{
public:
void remove_consumer(const Operator* c);
Operator* producer;
std::vector<Operator*> consumers;
int type;
std::vector<int> shape;
std::string name;
std::map<std::string, Parameter> params;
};
|
操作数结构中的producer和customers, 分别表示产生这个操作数的算子和使用这个操作数的算子。
值得注意的是产生这个操作数的算子只能有一个,而使用这个操作数的算子可以有很多个。
使用前,需要对PNNX::Operator再次封装
定义了一个名为RuntimeOperator的结构体。结构体包含以下成员变量:
-
name: 运算符节点的名称,可以用来区分一个唯一节点,例如 Conv_1, Conv_2 等;
-
type: 运算符节点的类型,例如 Convolution, Relu 等类型;
-
layer: 负责完成具体计算的组件,例如在 Convolution Operator 中,layer 对输入进行卷积计算,即计算其相应的卷积值;
-
input_operands 和 output_operands 分别表示该运算符的输入和输出操作数。
如果一个运算符(RuntimeOperator)的输入大小为 (4, 3, 224, 224),那么在 input_operands 变量中,datas 数组的长度为 4,数组中每个元素的张量大小为 (3, 224, 224);
-
params 是运算符(RuntimeOperator)的参数信息,包括卷积层的卷积核大小、步长等信息;
-
attribute 是运算符(RuntimeOperator)的权重、偏移量信息,例如 Matmul 层或 Convolution 层需要的权重数据;
-
其他变量的含义可参考注释。
按照要求,需要将PNNX中的Operator封装到到新的RuntimeOperator
具体来说,有三个方面:
- 提取PNNX中的操作数Operand到RuntimeOperand
- 提取PNNX中的权重(Attribute)到RuntimeAttribute
- 提取PNNX中的参数(Param)到RuntimeParam(作业)
作业代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
|
/// 提取PNNX中的操作数Operand到RuntimeOperand 包含(InitGraphOperatorsInput)和(InitGraphOperatorsOutput)两个函数
/// 两个参数分别为运算符的所有输入操作数 Operand 和待初始化的 RuntimeOperator
void RuntimeGraph::InitGraphOperatorsInput(
const std::vector<pnnx::Operand *> &inputs,
const std::shared_ptr<RuntimeOperator> &runtime_operator) {
// 遍历所有输入的张量
for (const pnnx::Operand *input: inputs) {
if (!input) {
continue;
}
const pnnx::Operator *producer = input->producer;
std::shared_ptr<RuntimeOperand> runtime_operand =
std::make_shared<RuntimeOperand>();
// 搬运name和shape
runtime_operand->name = producer->name;
runtime_operand->shapes = input->shape;
switch (input->type) {
case 1: {
// 搬运类型
runtime_operand->type = RuntimeDataType::kTypeFloat32;
break;
}
case 0: {
runtime_operand->type = RuntimeDataType::kTypeUnknown;
break;
}
default: {
LOG(FATAL) << "Unknown input operand type: " << input->type;
}
}
runtime_operator->input_operands.insert({producer->name, runtime_operand});
runtime_operator->input_operands_seq.push_back(runtime_operand);
}
}
/// 两个参数分别为运算符的所有输出操作数 Operand 和待初始化的 RuntimeOperator
void RuntimeGraph::InitGraphOperatorsOutput(
const std::vector<pnnx::Operand *> &outputs,
const std::shared_ptr<RuntimeOperator> &runtime_operator) {
for (const pnnx::Operand *output: outputs) {
if (!output) {
continue;
}
const auto &consumers = output->consumers;
for (const auto &c: consumers) {
runtime_operator->output_names.push_back(c->name);
}
}
}
/// 提取PNNX中的参数(Param)到RuntimeParam
void RuntimeGraph::InitGraphParams(
const std::map<std::string, pnnx::Parameter> ¶ms,
const std::shared_ptr<RuntimeOperator> &runtime_operator) {
// 一个名字对应一个data
for (const auto &[name, parameter]:params) {
//拷贝类型
const int type = parameter.type;
// 0=null 1=b 2=i 3=f 4=s 5=ai 6=af 7=as 8=others
switch (type) {
case int(RuntimeParameterType::kParameterUnknown): {
// 创建一个空的RuntimeParameter类型的数据,因为数据为空,直接插入
RuntimeParameter *runtime_parameter = new RuntimeParameter;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterBool): {
RuntimeParameterBool *runtime_parameter = new RuntimeParameterBool;
runtime_parameter->value = parameter.b; //拷贝数据
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterInt): {
RuntimeParameterInt *runtime_parameter = new RuntimeParameterInt;
runtime_parameter->value = parameter.i;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterFloat): {
RuntimeParameterFloat *runtime_parameter = new RuntimeParameterFloat;
runtime_parameter->value = parameter.f;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterString): {
RuntimeParameterString *runtime_parameter = new RuntimeParameterString;
runtime_parameter->value = parameter.s;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterIntArray): {
RuntimeParameterIntArray * runtime_parameter = new RuntimeParameterIntArray;
runtime_parameter->value = parameter.ai;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterFloatArray): {
RuntimeParameterFloatArray *runtime_parameter = new RuntimeParameterFloatArray;
runtime_parameter->value = parameter.af;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterStringArray): {
RuntimeParameterStringArray *runtime_parameter = new RuntimeParameterStringArray;
runtime_parameter->value = parameter.as;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
default: {
LOG(FATAL) << "Unknown parameter type: " << type;
}
}
}
}
|
四:构建计算图关系和执行顺序
深度学习模型是一个有向无环图。对于有向图结构中的节点,可以认为是深度学习模型中的计算节点(算子),而有向图结构中的边可以认为是算子之间连接和前后依赖关系。
步骤:
- 计算图初始化(第三节的内容)
- 计算图的构建
- 计算图的顺序执行(递归方法)
我们通常使用拓扑排序来找到一个节点序列,在序列中每个节点的前驱节点都能排在这个节点的前面。
基于深度优先的拓扑排序计算步骤
- 选定一个入度为零的节点(
current_op),入度为零指的是该节点没有前驱节点或所有前驱节点已经都被执行过,在选定的同时将该节点的已执行标记置为True,并将该节点传入到ReverseTopo函数中;
- 遍历1步骤中节点的后继节点(
current_op->output_operators);
- 如果1的某个后继节点没有被执行过(已执行标记为
False),则递归将该后继节点传入到ReverseTopo函数中;
- 第2步中的遍历结束后,我们将当前节点放入到执行队列(
topo_operators_)中。
计算图递归执行的程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
void RuntimeGraph::ReverseTopo(
const std::shared_ptr<RuntimeOperator> &root_op) {
CHECK(root_op != nullptr) << "current operator is nullptr";
root_op->has_forward = true; // 将已执行的标志设置为true
const auto &next_ops = root_op->output_operators; // 后继节点
for (const auto &[_, op] : next_ops) { // 遍历后继节点
if (op != nullptr) {
if (!op->has_forward) { // 如果其中一个后继节点没有遍历过
this->ReverseTopo(op); // 则直接将该节点当做当前节点递归执行该程序
}
}
}
for (const auto &[_, op] : next_ops) {
CHECK_EQ(op->has_forward, true);
}
this->topo_operators_.push_back(root_op); // 将没有后继节点的节点放入root_op中
}
|
使用一个简单的计算图例子来走一下上述过程:
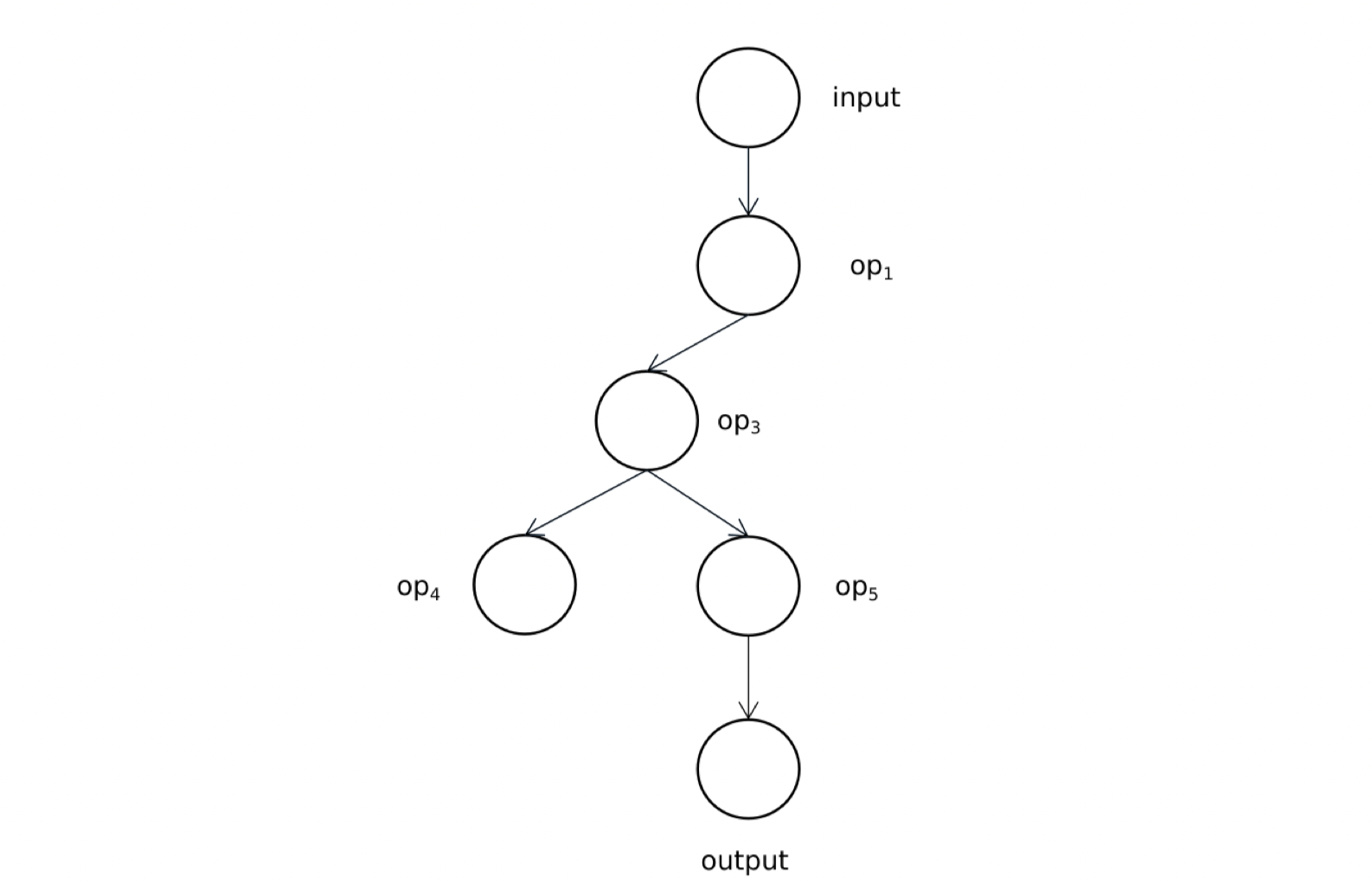
执行队列的顺序:
按照执行顺序,首先没有后继节点的是op4,第二个没有后继节点的为output。
[op4,output,op5,op3,op1,input],逆序之后,真正的执行顺序为[input,op1,op3,op5,output, op4]。
模型的状态
RuntimeGraph一共有三种状态,表示同一个模型的不同状态(待初始化,待构建,构建完成):
1
2
3
4
5
|
enum class GraphState {
NeedInit = -2;
NeedBuild = -1;
Complete = 0,
};
|
在初始情况下模型的状态graph_state_为NeedInit,表示模型目前待初始化。因此我们不能在此刻直接调用Build函数中的功能,而是需要在此之前先调用模型的Init函数,在初始化函数(Init)调用成功后会将模型的状态调整为NeedBuild.
1
|
NeedInit ---> NeedBuild ---> Complete
|
构建图关系
该部分代码为:
1
2
3
4
5
6
7
8
9
10
11
12
|
// 构建图关系
for (const auto ¤t_op : this->operators_) {
// 获取当前节点的所有后继节点的names,遍历根据next_op_name从operators_maps_中插入所需要的节点
const std::vector<std::string> &output_names = current_op->output_names;
for (const auto &kOutputName : output_names) {
if (const auto &output_op = this->operators_maps_.find(kOutputName);
output_op != this->operators_maps_.end()) {
// output_operator 代表该节点的后继节点
current_op->output_operators.insert({kOutputName, output_op->second});
}
}
}
|
可以看到每次都是通过节点的names,遍历根据next_op_name,然后插入该节点的后继节点。
节点输出张量的初始化
我们在Build函数中还需要完成计算节点中输出张量空间的初始化,这样是为了节省运行时申请内存需要的时间,从下图中可以看出每个节点都有一个形状不同的输出张量,用来存放该节点的计算输出。
那为什么我们不需要对输入空间进行初始化呢?
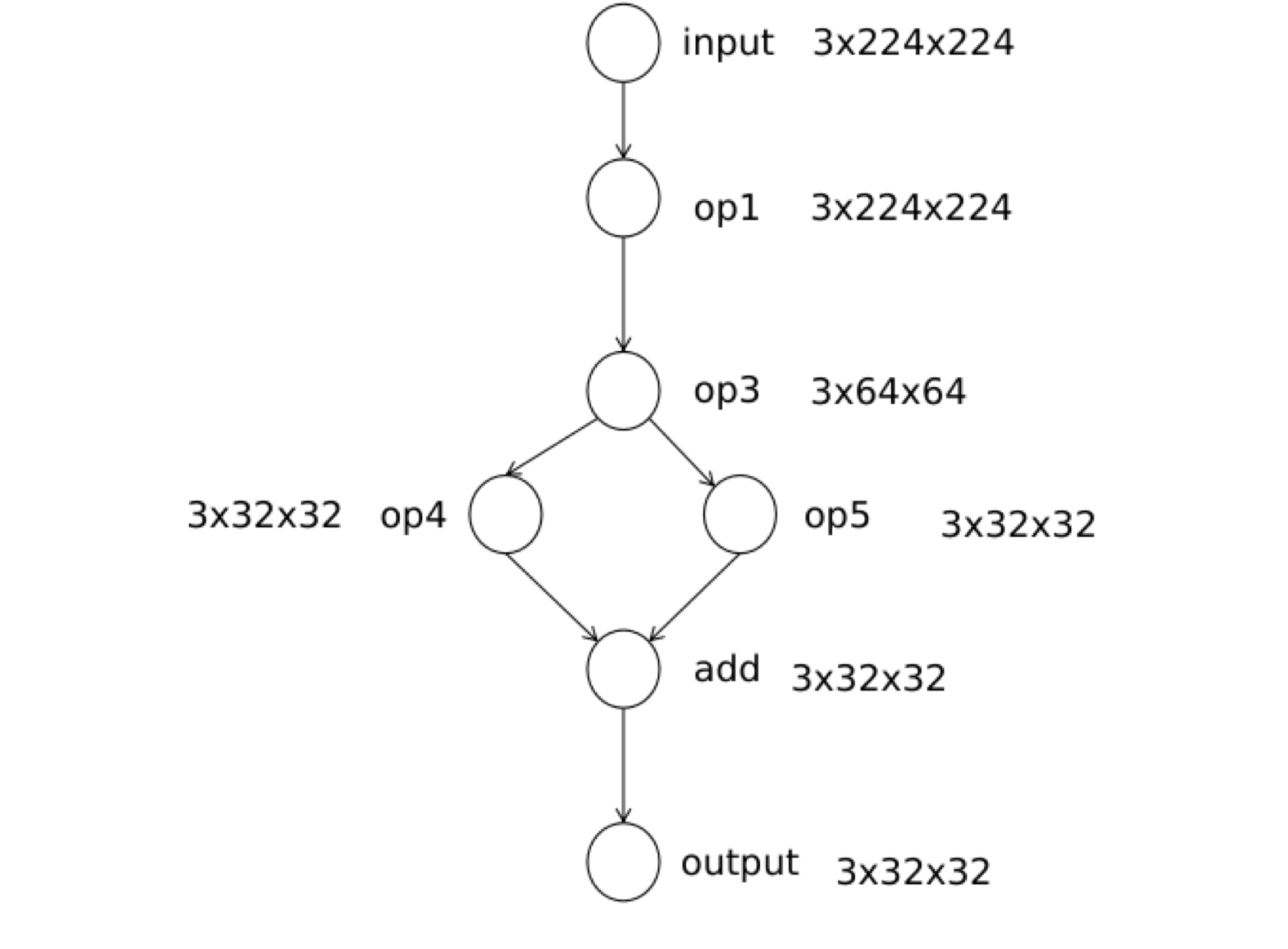
主要的原因就是每个节点的输出空间和下个节点的输入是相同的,所以不需要申请额外的空间。
其中的函数是:
1
2
|
// 第一个参数是pnnx的计算节点 ,第二个参数是RuntimeGraph的计算节点
InitOperatorOutput(graph_->ops, operators_);
|
具体代码很长,其具体过程:
- 先判断PNNX和Runtime_op是否等长
- 获得第i个计算节点中的所有输出计算数
operand, 我们需要根据这个pnnx计算数Operand中记录的Shape和Type信息来初始化我们runtime_op中输出数据存储的空间
- 我们输出张量的维度只支持二维的、三维以及四维的,所以需要在以上代码上做
check.
- 初始化结构中存放输出数据的
datas变量,它是一个张量的数组类型,数组的长度等于该计算节点的batch_size大小。
- 在循环后结束后,我们会将初始化好的
output_operands绑定到对应的计算节点中用于保存计算节点的输出数据。
作业:使用另一种方式实现拓扑排序(不使用递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
void RuntimeGraph::ReverseTopo(const std::shared_ptr<RuntimeOperator> &root_op) {
CHECK(root_op != nullptr) << "current operator is nullptr";
std::stack<std::shared_ptr<RuntimeOperator>> stack;
stack.push(root_op);
while(!stack.empty()) {
auto current_op = stack.top();
stack.pop();
if(!current_op->has_forward){ //其中一个后继节点没有遍历过
current_op->has_forward = true;
const auto& next_ops = current_op->output_operators;
for (const auto&[_, op] : next_ops) {
if (op != nullptr && !op->has_forward){
stack.push(op);
}
}
for (const auto &[_, op] : next_ops) {
CHECK_EQ(op->has_forward, true);
}
}
}
}
|
五:算子和注册工厂
一个完整的计算图,包括了输入、输出节点以及计算节点等。计算节点在我们这个项目中被称之为RuntimeOperator, 具体的结构定义如下的代码所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
struct RuntimeOperator {
virtual ~RuntimeOperator();
bool has_forward = false;
std::string name; /// 计算节点的名称
std::string type; /// 计算节点的类型
std::shared_ptr<Layer> layer; /// 节点对应的计算Layer
std::map<std::string, std::shared_ptr<RuntimeOperand>>
input_operands; /// 节点的输入操作数
std::shared_ptr<RuntimeOperand> output_operands; /// 节点的输出操作数
std::vector<std::shared_ptr<RuntimeOperand>>
input_operands_seq; /// 节点的输入操作数,顺序排列
std::map<std::string, std::shared_ptr<RuntimeOperator>>
output_operators; /// 输出节点的名字和节点对应
...
|
现在我们要实现Layer的功能,其作用其实就是进行计算,为所有算子的父类。
其整体的工作流程为:通过访问RuntimeOperator的输入数(input_operand),layer可以获取计算所需的输入张量数据,并根据layer各派生类别中定义的计算函数(forward)对输入张量数据进行计算。计算完成后,计算结果将存储在该节点的输出数(output_operand)中。
流程图如下所示:
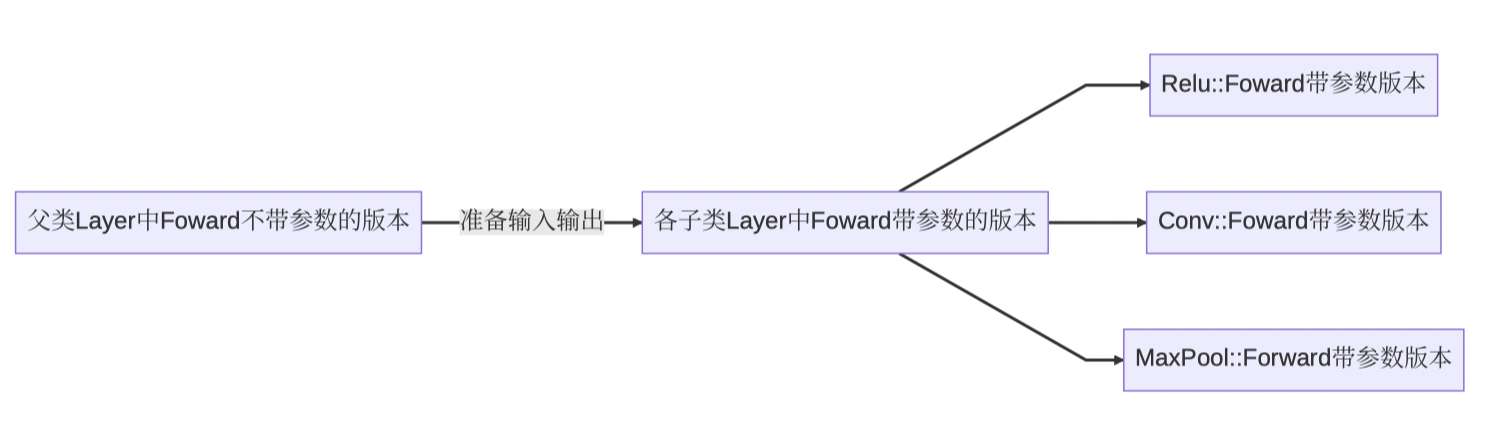
各个类与方法的关系如下:
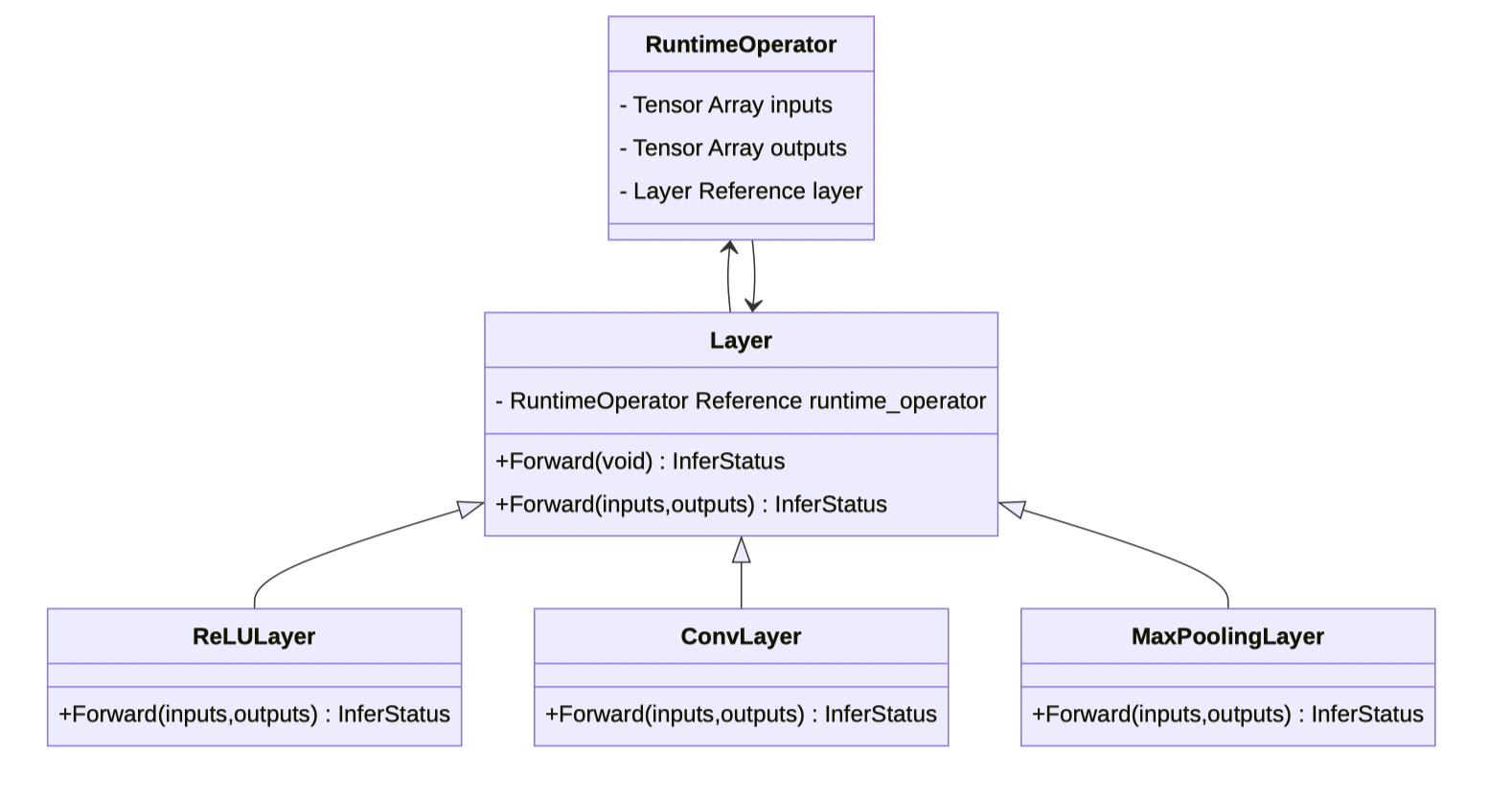
RuntimeOperator会去调用Layer类中的forward方法,forward方法则会去调用子方法。
其中不带参数的forward版本的调用流程如下:
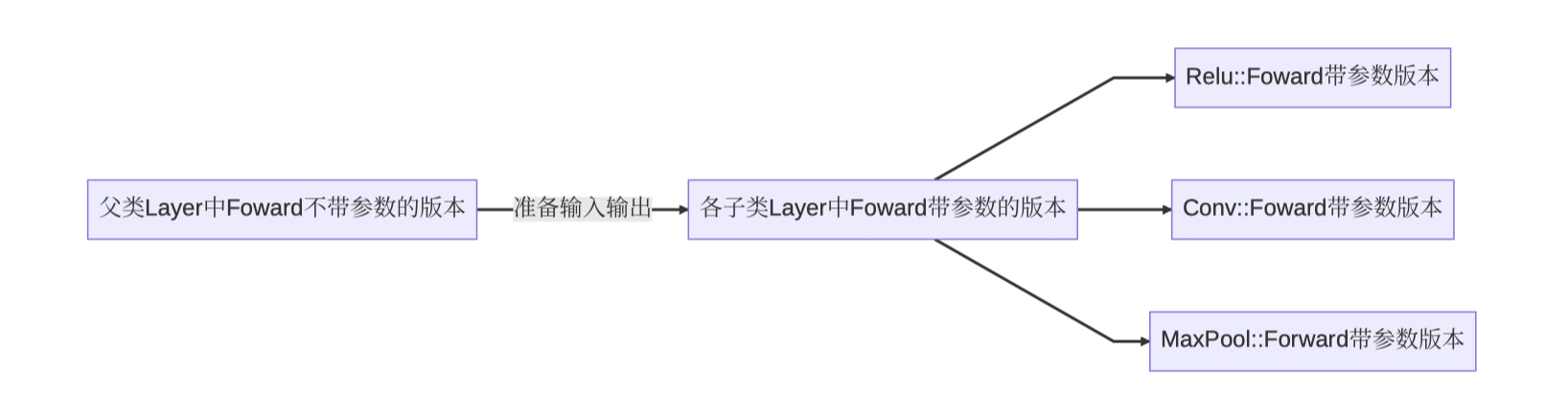
这里的准备输入输出是在父类Layer中进行的!
如何解决多个前置输入节点的计算问题
input_operand_datas存放了所有的输入数据,通过循环的方式将所有数据平铺放入Layer类中的变量layer_input_data中。同样的,参数outputs存放输出的结果,是一个预申请的空间,从Layer相关联的Runtime_Operater类中的output_operand作为输出数组。
全局算子注册器
在KuiperInfer中算子注册机制使用了单例模式和工厂模式。首先,在全局范围内创建一个唯一的注册表registry,它是一个map实现的。这个注册表的键是算子的类型,而值是算子的初始化过程,初始化过程的值具体是一个函数指针。
开发者完成一个算子的开发后,需要通过特定的注册机制将算子写入全局注册表中。需要使用某个算子时,可以根据算子的类型从全局注册表中方便地获取对应的算子。
当支持的算子被添加到注册表之后,可以使用registry.find(layer_type)来获取特定类型算子的初始化过程,并调用该过程来获取相应算子的实例。
1
2
3
4
5
6
|
typedef ParseParameterAttrStatus (*Creator)
(const std::shared_ptr<RuntimeOperator> &op,std::shared_ptr<Layer> &layer) {
// 实例化一个layer的空指针,由于这里是示例,没有用到op的各种信息
layer = std::make_shared<Layer>("test_layer");
return ParseParameterAttrStatus::kParameterAttrParseSuccess;
}
|
这个初始化函数有两个参数,op记录了算子初始化需要的各种变量(参数、权重等等),layer位一个待初始化的空指针。
从注册器中取出算子
正如上面所说,因为注册器本质上是一个map,我们可以通过registry.find(layer_type)->second来取出算子的初始化过程。
ReLU算子的实现
ReLU的计算过程非常简单,有如下的定义:$ReLU(x)=max(x,0)$.
根据公式$ReLU(x) = max(x,0)$可以看出,ReLU算子不会改变输入张量的大小,也就是说输入和输出张量的维度应该是相同的。因此,代码逻辑: 首先检查输入数组是否为空,然后检查输入数组和输出数组中的元素(张量)个数是否相同,如果不满足该条件,程序返回并记录相关错误日志。
作业:Sigmoid算子实现
Sigmoid.hpp:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#ifndef KUIPER_DATAWHALE_SIGMOID_HPP
#define KUIPER_DATAWHALE_SIGMOID_HPP
#include "layer/abstract/non_param_layer.hpp"
namespace kuiper_infer{
class SigmoidLayer : public NonParamLayer{
public:
SigmoidLayer() : NonParamLayer("Sigmoid"){}
InferStatus Forward(
const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
std::vector<std::shared_ptr<Tensor<float>>>& outputs) override;
static ParseParameterAttrStatus GetInstance(
const std::shared_ptr<RuntimeOperator>& op,
std::shared_ptr<Layer>& sigmoid_layer);
};
} // namespace kuiper_infer
#endif //KUIPER_DATAWHALE_SIGMOID_HPP
|
Sigmoid.cpp:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
//
// Created by 蔡雄江 on 2023/9/5.
//
#include "sigmoid.hpp"
#include "layer/abstract/layer_factory.hpp"
namespace kuiper_infer {
InferStatus SigmoidLayer::Forward(const std::vector<std::shared_ptr<Tensor<float>>> &inputs,
std::vector<std::shared_ptr<Tensor<float>>> &outputs) {
//判断输入是否为空
if (inputs.empty()) {
LOG(ERROR) << "The input tensor array in the sigmoid layer is empty";
return InferStatus::kInferFailedInputEmpty;
}
// 判断输入输出维度是否相同
if (inputs.size() != outputs.size()) {
LOG(ERROR) << "The input and output tensor array size of the sigmoid layer do not match";
return InferStatus::kInferFailedInputOutSizeMatchError;
}
const uint32_t batch_size = inputs.size();
for (uint32_t i = 0; i < batch_size; ++i) {
const sftensor &input_data = inputs.at(i);
const sftensor &output_data = outputs.at(i);
// 判断每一个batch是否为空
if (input_data == nullptr || input_data->empty()) {
LOG(ERROR)
<< "The input tensor array in the sigmoid layer has an empty tensor "
<< i << " th";
return InferStatus::kInferFailedInputEmpty;
}
//判断每一个batch的维度是否相同
if (output_data != nullptr && !output_data->empty()) {
if (input_data->shapes() != output_data->shapes()) {
LOG(ERROR) << "The input and output tensor shapes of the sigmoid layer do not match "
<< i << " th";
return InferStatus::kInferFailedInputOutSizeMatchError;
}
}
}
for (uint32_t i = 0; i < batch_size; ++i) {
const std::shared_ptr<Tensor<float>> &input = inputs.at(i); // 输入是保持不变的
CHECK(input != nullptr || !input->empty())
<< "The input tensor array in the sigmoid layer has an empty tensor "
<< i << " th";
std::shared_ptr<Tensor<float>> output = outputs.at(i); // 输出是要改变的,所以是变量
if (output == nullptr || output->empty()) {
DLOG(ERROR) << "The output tensor array in the sigmoid layer has an empty tensor "
<< i << " th";
output = std::make_shared<Tensor<float>>(input->shapes());
outputs.at(i) = output;
}
CHECK(output->shapes() == input->shapes())
<< "The input and output tensor shapes of the sigmoid layer do not match "
<< i << " th";
/// Sigmoid算子的运算逻辑(取出一个张量的一个数据,进行运算)
for (uint32_t j = 0; j < input->size(); ++j) {
float value = input->index(j);
output->index(j) = 1 / (1.f + expf(-value));
}
}
return InferStatus::kInferSuccess;
}
/// 实例化函数
ParseParameterAttrStatus SigmoidLayer::GetInstance(
const std::shared_ptr<RuntimeOperator> &op,
std::shared_ptr<Layer> &sigmoid_layer) {
CHECK(op != nullptr) << "Sigmoid operator is nullptr";
sigmoid_layer = std::make_shared<SigmoidLayer>();
return ParseParameterAttrStatus::kParameterAttrParseSuccess;
}
/// 使用工具类注册算子
LayerRegistererWrapper kSigmoidGetInstance("nn.Sigmoid", SigmoidLayer::GetInstance);
}
|
六:卷积和池化算子的实现
池化算子实现
池化算子按照类型可以分为平均池化和最大池化,池化算子需要确定的参数有步长(stride height),窗口大小(pooling height、pooling width),其顺序一般是从左到右,从上到下。
输入大小和输出大小之间有这样的关系:
$$
output\ size = floor(\frac{input\ size - pooling\ size}{stride} + 1)
$$
$4\times 4$的按照大小为2,stride为2的池化后,特征图的大小减小了2倍。
当池化中加入了Padding后,等式发生了一些改变:
$$
output\ size = floor(\frac{input\ size + 2 \times padding- pooling\ size}{stride} + 1)
$$
对于多通道的池化只是单通道池化的堆叠。
- 使用最大池化举例,如何定位输出张量的具体位置,并进行赋值:
output_data->slice(ic)获取第ic个输出张量output_channel.colptr(int(c / stride_w_));计算第ic个张量的输出列位置*(output_channel_ptr + int(r / stride_h_)) = max_value,将对应位置的值使用最大值填充。
池化算子的注册和实例化
MaxPoolingLayer::GetInstance:
1
2
|
LayerRegistererWrapper kMaxPoolingGetInstance("nn.MaxPool2d",
MaxPoolingLayer::GetInstance);
|
具体的实例化函数如下:
1
2
3
4
5
6
|
ParseParameterAttrStatus MaxPoolingLayer::GetInstance(
const std::shared_ptr<RuntimeOperator>& op,
std::shared_ptr<Layer>& max_layer) {
...
const std::map<std::string, std::shared_ptr<RuntimeParameter>>& params =
op->params;
|
卷积算子的实现
我们这里以二维的输入为主,此处以单通道为例:
$$
Y[i, j] = \sum_{m} \sum_{n} H[m, n] \cdot X[i+m, j+n]
$$
其中,$X$表示输入矩阵,$H$表示卷积核,$Y$表示输出矩阵,$i$和$j$表示输出矩阵中的输出像素坐标,$m$和$n$表示卷积核中的坐标,$i+m$和$j+n$用于将卷积核和输入矩阵进行对齐,分别表示输入图像中的某个元素坐标。通过这两个偏移量,我们可以确定卷积核在输入矩阵中的位置,并将其与对应位置的像素值相乘,然后求和得到输出矩阵的每个元素 $Y[i,j]$。
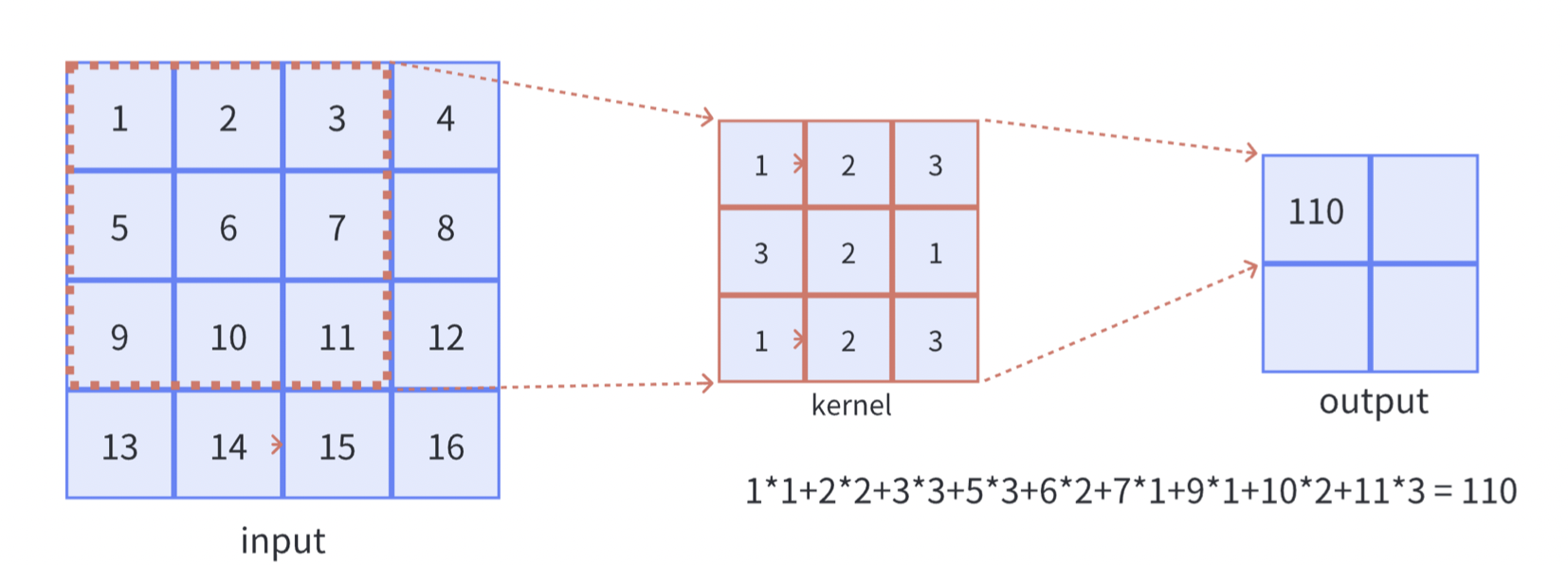
其中i、j其实代表的是卷积核的位置(左上角),而m和n代表的是卷积核内的偏移量。
**如果输入改为多通道,最后得到一个单通道,需要如何处理?**如下图所示:
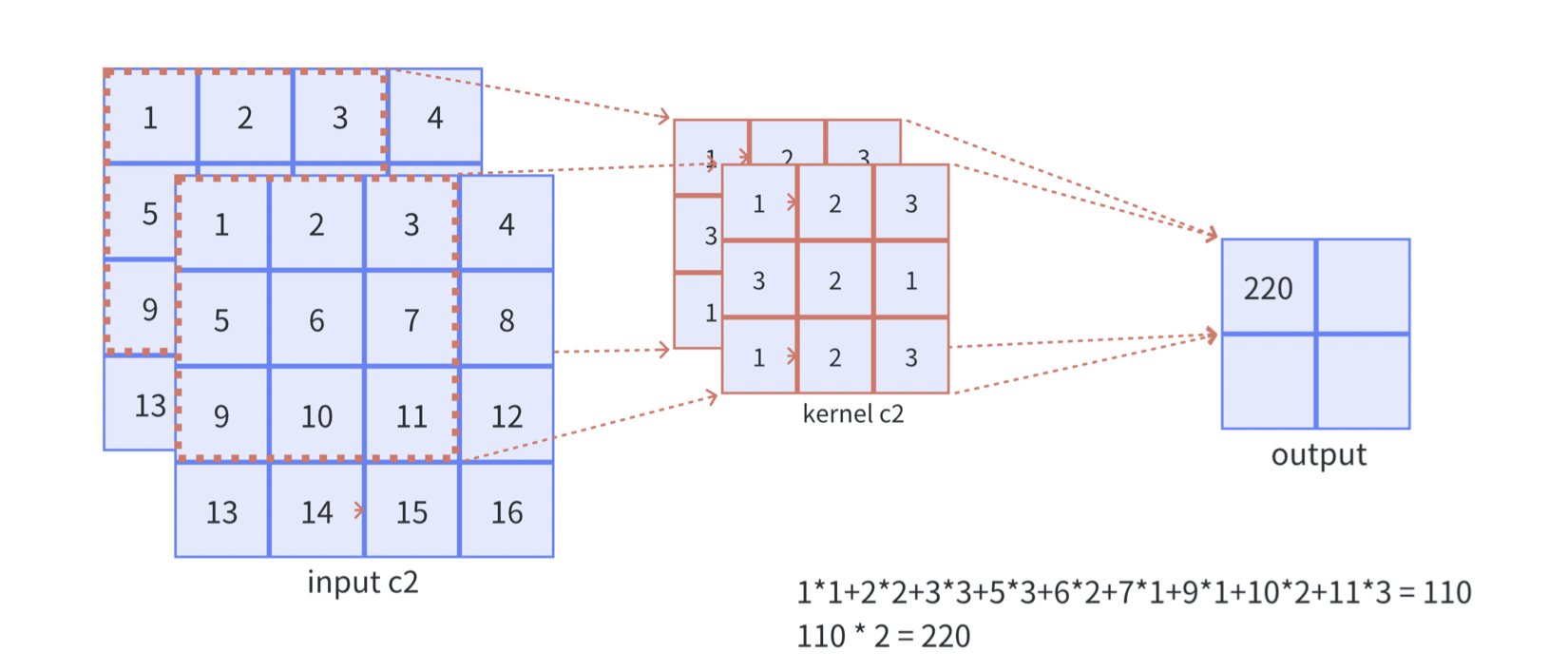
需要注意的是,这里只有一个卷积核,画成两个是因为重复计算了(这里假设张量有两个通道)!
如果输出改成了多通道,那么卷积核的个数就要增加,如图所示:

从上面的过程可以看出,二维卷积的计算如下:
$$
output, size = floor(\frac{input,size+ 2\times padding-kernel ,size}{stride }+1)
$$
可以发现和池化算子的输入输出大小计算是非常相似的!
im2col优化卷积计算
其核心思想是将卷积计算转化为矩阵计算,利用现有的矩阵加速方法实现卷积运算的加速。
举一个具体的例子就可以明白,其实就是将一个卷积核大小的张量进行展开成为矩阵中的一行,如图所示:
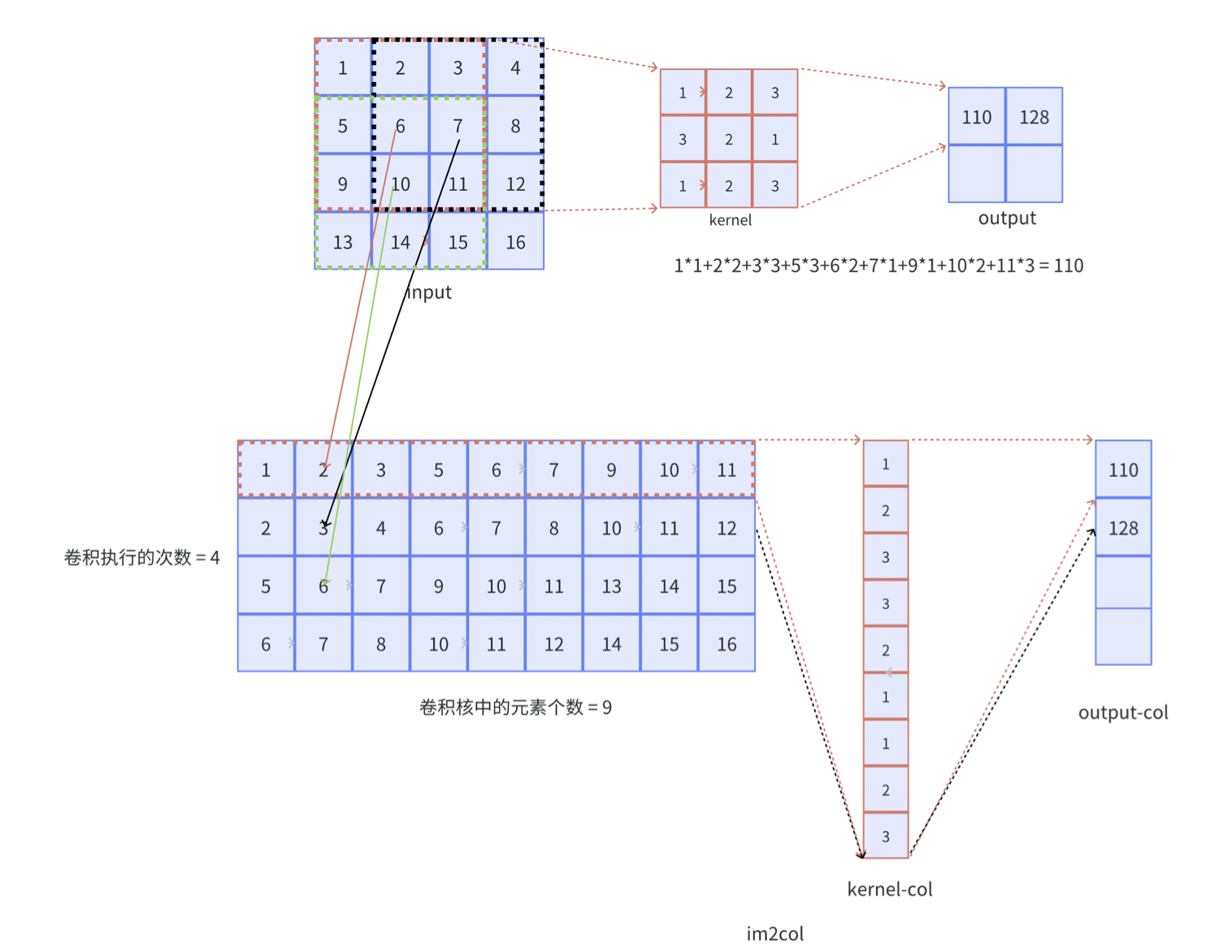
如果对于多通道的输入,需要如何进行优化呢?
其实很简单,就是将每个通道的矩阵进行平铺,而卷积核则进行列铺就ok了:
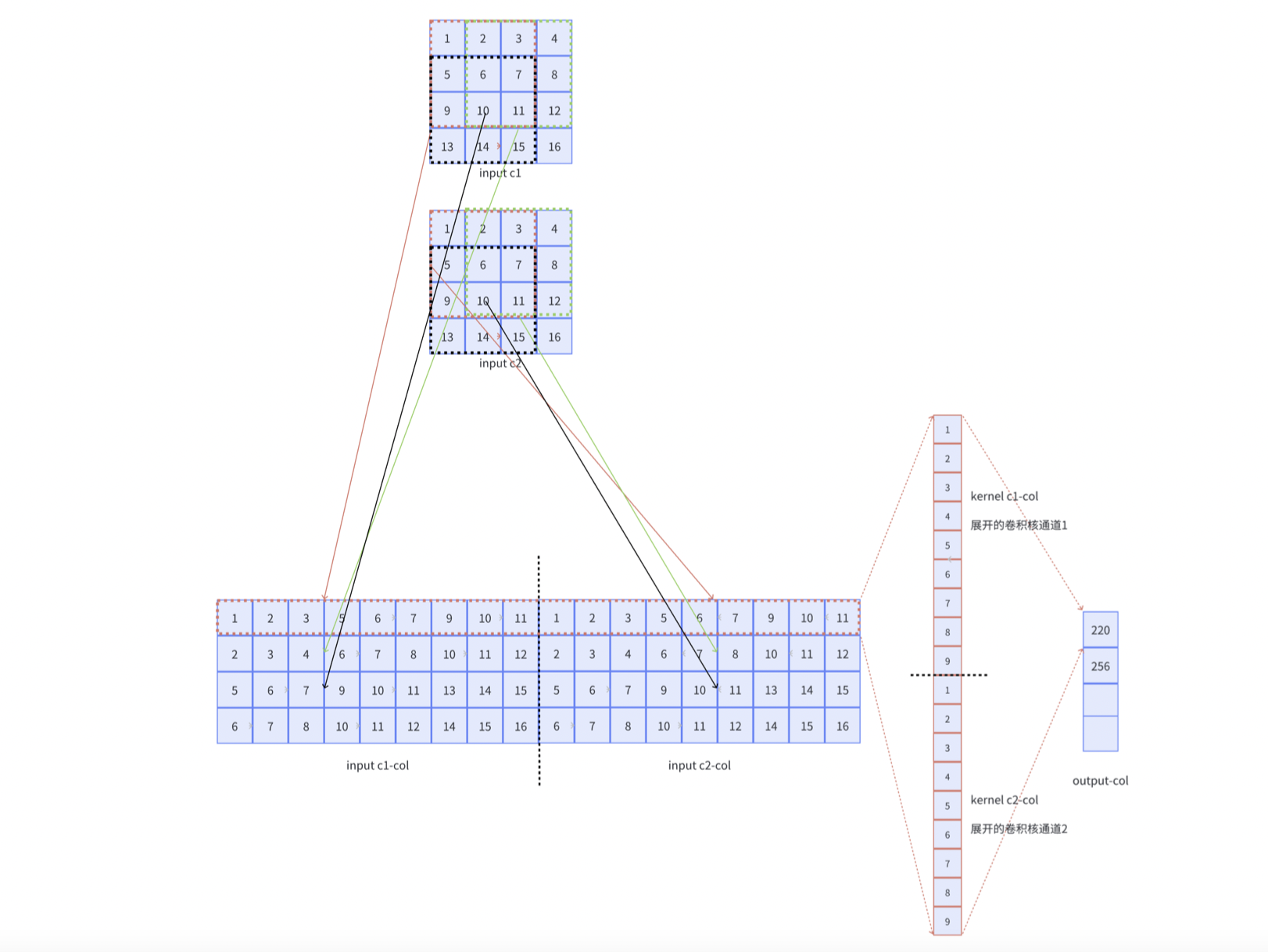
输出张量也变为多通道,则增加卷积核的个数,也就是增加卷积核张开的张量的列数:
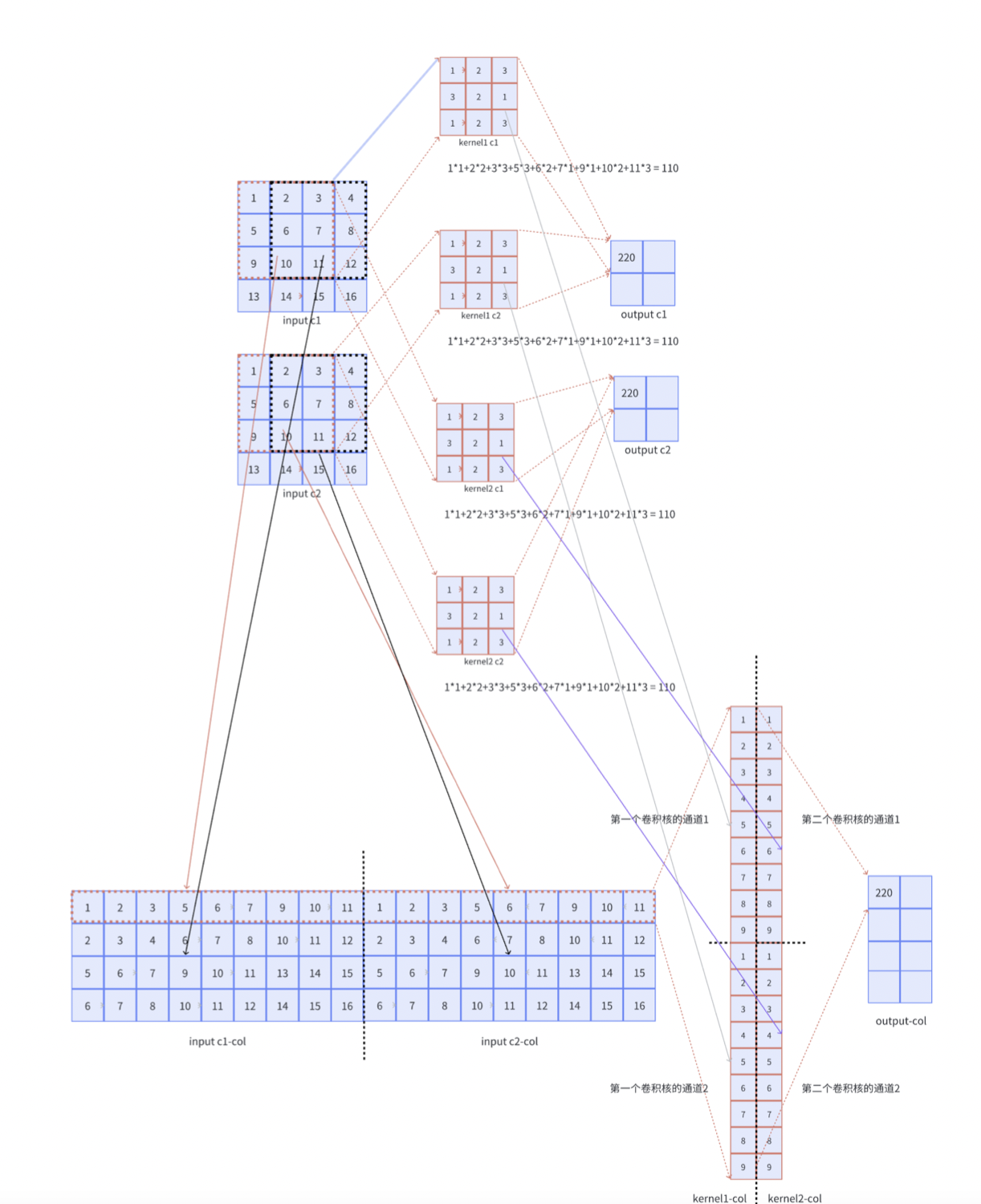
分组卷积的实现
假设group 的数量为2,如果输入特征图的通道数为4,共有4个卷积核。
那么输入特征图的4个通道被分为2组,每组的输入通道数为2,卷积核也被分为两组,每组的卷积核个数也是2!
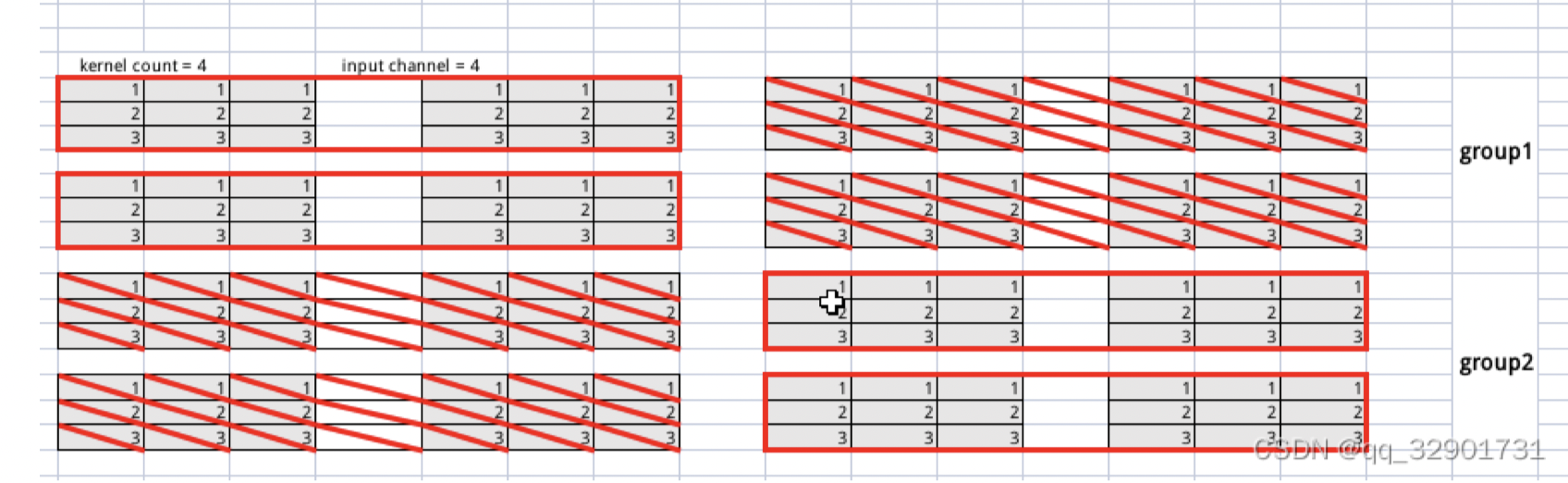
一个红框代表一个卷积核,画两次是因为输入张量每组的通道数为2,则需要重复计算两次!上述图中有4个卷积核,分别处理channel为0,1,2,3的输入通道数!可以看到分组卷积相对普通卷积少了2倍,也就是输入张量每次需要处理的通道数减少了一半,卷积核的总数是不变的!
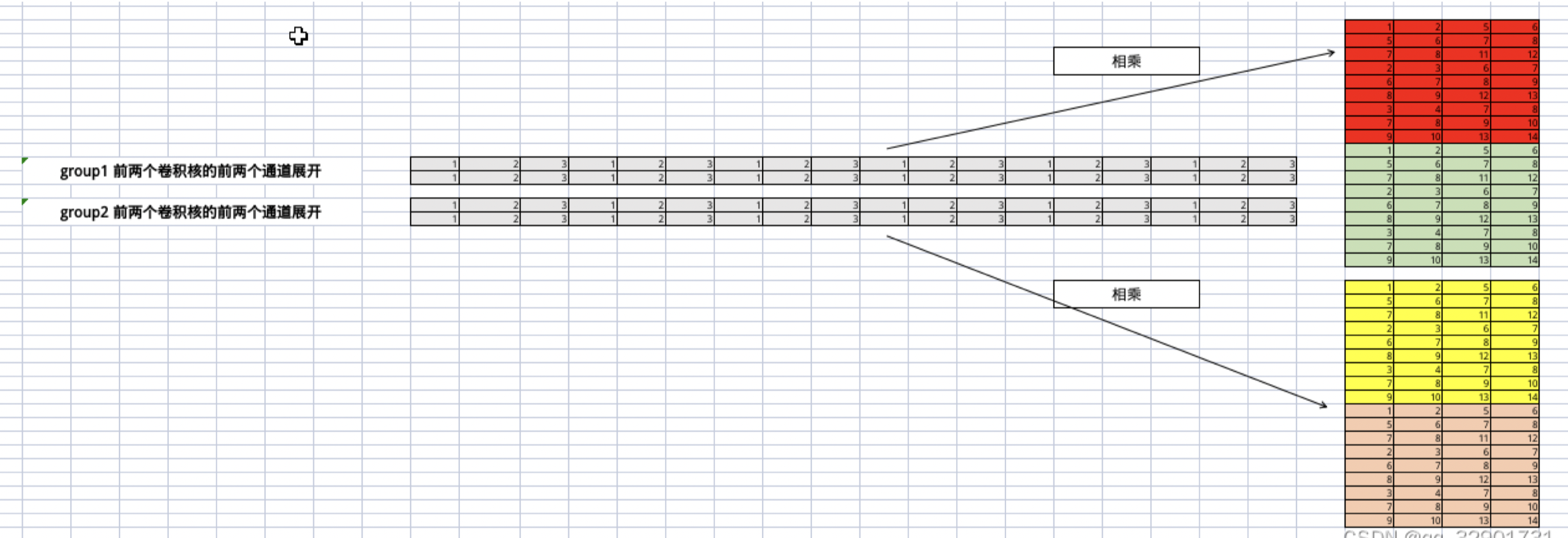
展开之后如上图所示,只是这里为了方便,把卷积核的展开放在了前面且变成行展开,原理是一样的。
假设单输入单输出通道的卷积计算量为X,那么原先4输出4输出的的计算量为16X,分组卷积变为了$2\times 2 + 2\times 2=8$,8X的计算量。
因为我们的armadillo自身是列主序的,所以im2Col自然就变为了im2Row!
参数汇总
那么实现上述功能的卷积,需要的参数有:
-
input: 输入特征图像
-
kernel_*: 卷积核的大小
-
input_*: 输入特征图像的尺寸大小,也就是input的尺寸大小
-
input_c_group: 每个group处理的通道数量,如前文所叙,我们会将输入特征图的通道按照组数进行切分
-
group: 当前进行Im2Col的组数(group)
-
row_len: $kernel_w\times kernel_h$, 也就是一个卷积窗口展开后的行长度(下图中的9)。
-
col_len: 卷积滑动的次数,也就是**卷积窗口滑动的次数,或者是一个通道输入展开后的列长度*(下图中的4)。*
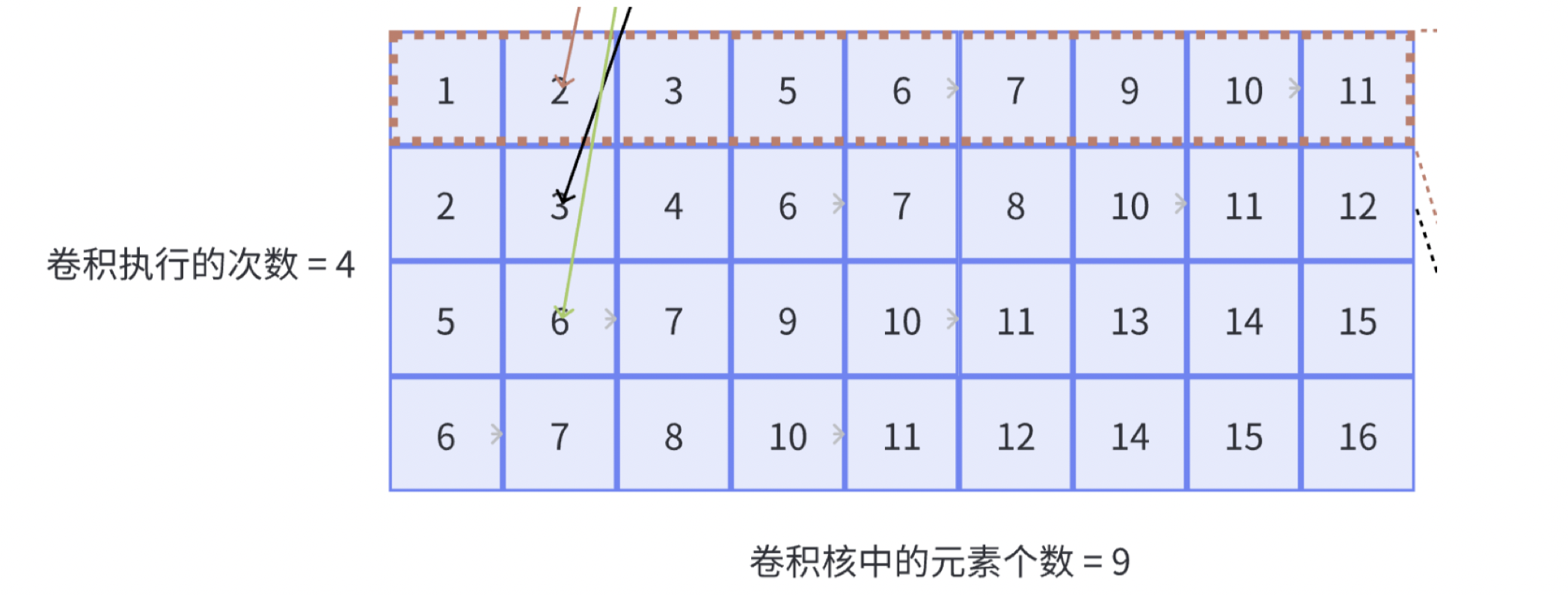
1
2
3
|
arma::fmat input_matrix(input_c_group * row_len, col_len);
const uint32_t input_padded_h = input_h + 2 * padding_h_;
const uint32_t input_padded_w = input_w + 2 * padding_w_;
|
input_matrix用于存储对输入图像展开后的矩阵, input_padded_*表示输入填充后的尺寸大小。为什么这里的input_matrix行数等于$input_c_group\times row_len$呢,我们从下方的图中可以看出,对于多输入通道的情况,它的列数等于输入通道数和卷积核相乘(因为我们是列主序的,实际执行Im2Row,所以行列相反),它的行数等于col_len(行列相反),也就是卷积窗口进行滑动的次数。
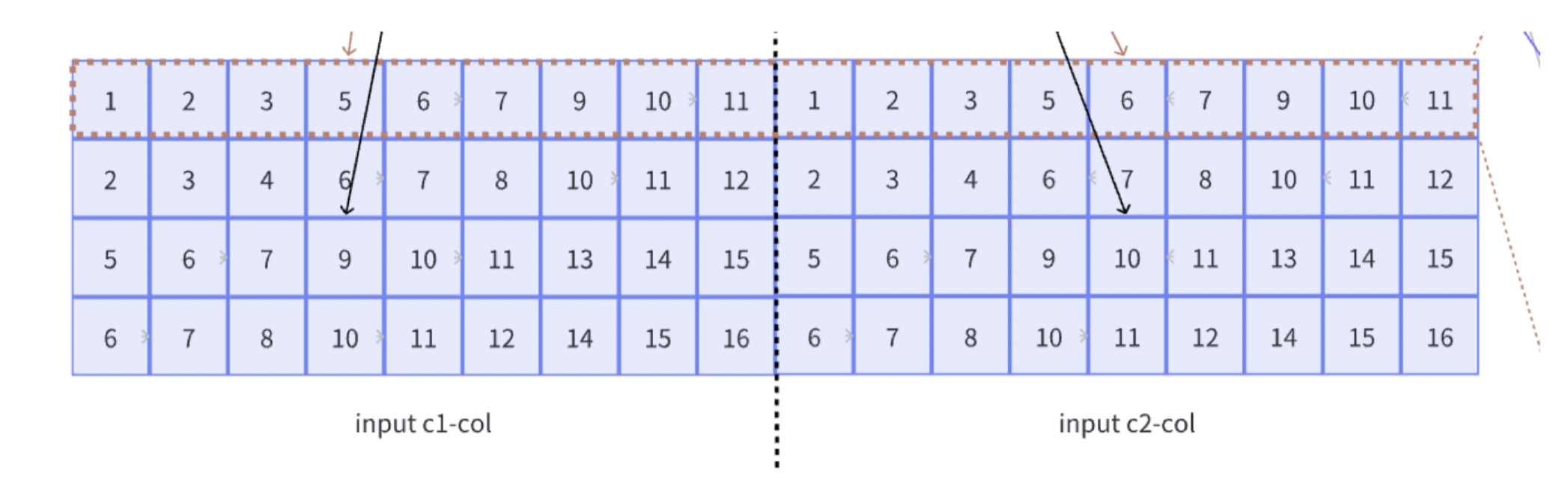
接下去就将输入的卷积区域展开为矩阵,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
for (uint32_t ic = 0; ic < input_c_group; ++ic) {
// 获取当前通道的输入
float* input_channel_ptr =
input->matrix_raw_ptr(ic + group * input_c_group);
uint32_t current_col = 0;
// 当前通道的展开应该放在哪个行位置
// 因为多个通道同一位置是横向摆放的
uint32_t channel_row = ic * row_len;
// 表示在一个输入通道上进行滑动
for (uint32_t w = 0; w < input_padded_w - kernel_w + 1; w += stride_w_) {
for (uint32_t r = 0; r < input_padded_h - kernel_h + 1; r += stride_h_) {
float* input_matrix_ptr =
input_matrix.colptr(current_col) + channel_row;
···
|
后面就是实现矩阵内部的处理了,不再描述。
卷积算子实现的流程
-
对批次数据逐个处理(按Batch Size的大小做循环)
-
计算输入输出张量的尺寸、以及卷积窗口执行的次数(col_len)
-
对group进行迭代遍历,g表示当前组号,input_c_group表示每组卷积需要处理的通道数,Im2Col函数中会对属于该组的输入通道进行展开。
-
随后进行矩阵相乘的操作
KuiperInfer中的GEMM实现(矩阵乘法操作)
1
2
3
4
5
|
void ConvolutionLayer::ConvGemmBias(
const arma::fmat& input_matrix, sftensor output_tensor, uint32_t group,
uint32_t kernel_index, uint32_t kernel_count_group,
const arma::frowvec& kernel, uint32_t output_w, uint32_t output_h) const {
···
|
传入到这个函数中的参数,依次是:
input_matrix: 展开后的输入特征output_tensor: 用于存放输出的矩阵group: 当前进行Im2Col的组(group)数kernel* :用于定位当前展开后的卷积核output_*: 输出矩阵的尺度大小
这里只需要注意是否有bias需要分情况讨论即可
卷积算子的实例化
- 首先我们需要将Runtime_operator中的信息(
params)拿出来
- 加载卷积算子中的权重(
Attributes)
- 然后赋值给
Conv Layer进行初始化后,注册到算子工厂
因为对于一个卷积算子来说,它的输入是不确定的,所以我们需要在运行时再调用Im2Col进行展开,而一个卷积算子中的权重是固定的,所以可以在初始化的时候进行展开。
课程作业:调试代码 + 写group不为1的单元测试并进行调试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
/// group为2的情况 (通道数和卷积核个数必须为偶数)
TEST(test_registry, create_layer_convforward_group) {
const uint32_t batch_size = 1;
std::vector<std::shared_ptr<Tensor<float>>> inputs(batch_size);
std::vector<std::shared_ptr<Tensor<float>>> outputs(batch_size);
const uint32_t in_channel = 2;
for (uint32_t i = 0; i < batch_size; ++i) {
sftensor input = std::make_shared<ftensor>(in_channel, 4, 4);
input->data().slice(0) = arma::fmat("1,2,3,4;"
"5,6,7,8;"
"9,10,11,12;"
"13,14,15,16;");
input->data().slice(1) = arma::fmat("1,2,3,4;"
"5,6,7,8;"
"9,10,11,12;"
"13,14,15,16;");
inputs.at(i) = input;
}
const uint32_t kernel_h = 3;
const uint32_t kernel_w = 3;
const uint32_t stride_h = 1;
const uint32_t stride_w = 1;
const uint32_t kernel_count = 2;
const uint32_t group = 2; // 设置分组数为2
std::vector<sftensor> weights;
for (uint32_t i = 0; i < kernel_count; ++i) {
/// channel数计算: in_channel / group kernel的计算次数也要随着分组减少
sftensor kernel = std::make_shared<Tensor<float>>(in_channel / group, kernel_h, kernel_w); // 更新卷积核的通道数
kernel->data().slice(0) = arma::fmat("1,2,3;"
"3,2,1;"
"1,2,3;");
weights.push_back(kernel);
}
ConvolutionLayer conv_layer(kernel_count, in_channel, kernel_h, kernel_w, 0,
0, stride_h, stride_w, group, false); // 设置分组数
conv_layer.set_weights(weights);
conv_layer.Forward(inputs, outputs);
outputs.at(0)->Show();
}
|
七:表达式层的实现
表达式层的实现主要目的是为了折叠计算过程和消除中间变量。
PNNX中的表达式是一个二元计算过程,类似:
output_mid = input1 + input2;
output = output_mid * input3;
在PNNX的表达式层(Expression Layer)中,提供了一种计算表达式,该表达式能够在一定程度上折叠计算过程并消除中间变量。例如,在残差结构中的add操作在PNNX中就是一个表达式层。
下面是PNNX中对上述过程的计算表达式表示,其中的@0和@1代表之前提到的计算数RuntimeOperand,用于表示计算表达式中的输入节点。
mul(@2, add(@0, @1));
如果在表达式极为复杂的情况下,需要一个强大可靠的表达式解析和语法树构建功能。
词法定义
词法解析的目的是将**add(@0, mul(@1, @2))**拆分为多个Token,拆分后的Token依次为:
- Identifier: add
- Left bracket: (
- Input number: @0
- Comma: ,
- Identifier: mul
- Left bracket: (
- Input number: @1
- Comma: ,
- Input number: @2
- Right bracket: )
Token的类型定义如下:
1
2
3
4
5
6
7
8
9
|
enum class TokenType {
TokenUnknown = -9,
TokenInputNumber = -8,
TokenComma = -7,
TokenAdd = -6,
TokenMul = -5,
TokenLeftBracket = -4,
TokenRightBracket = -3,
};
|
Token的定义如下,包括以下变量:
- Token类型,包括add(加法),mul(乘法),bracket(左右括号)等;
- Token在原句子中的开始和结束位置,即
start_pos和end_pos;
对于表达式add(@0, mul(@1, @2)),我们可以将它切分为多个Token,其中Token(add)的start_pos为0,end_pos为3。Token(left bracket)的start_pos为3,end_pos为4。Token(@0)的start_pos为4,end_pos为5,以此类推。
1
2
3
4
5
6
7
8
9
10
|
// 词语Token
struct Token {
TokenType token_type = TokenType::TokenUnknown;
int32_t start_pos = 0; // 词语开始的位置
int32_t end_pos = 0; // 词语结束的位置
Token(TokenType token_type, int32_t start_pos, int32_t end_pos)
: token_type(token_type), start_pos(start_pos), end_pos(end_pos) {
}
};
|
最后,在词法解析结束后,我们还需要按照它们出现的顺序和层级关系组成一颗语法树。
1
2
3
4
5
6
7
8
9
|
// 语法树的节点
struct TokenNode {
int32_t num_index = -1;
std::shared_ptr<TokenNode> left = nullptr; // 语法树的左节点
std::shared_ptr<TokenNode> right = nullptr; // 语法树的右节点
TokenNode(int32_t num_index, std::shared_ptr<TokenNode> left,
std::shared_ptr<TokenNode> right);
TokenNode() = default;
};
|
词法解析
此部分可以看代码,在course7中的source/parser/parse_expression.cpp中。
语法解析
在进行语法分析时,我们可以根据词法分析得到的 token 数组构建抽象语法树。抽象语法树是一个由二叉树组成的结构,每个节点都存储了操作符号或值,并通过左子节点和右子节点与其他节点连接。
对于表达式 “add (@0, @1)",当 num_index 等于 1 时,表示计算数为 @0;当 num_index 等于 2 时,表示计算数为 @1。若 num_index 为负数,则说明当前节点是一个计算节点,如 “mul” 或 “add” 等。
以下是一个简单的示例:
add
/ \
@0 @1
在这个示例中,根节点是 “add”,左子节点是 “@0”,右子节点是 “@1”。这个抽象语法树表示了一个将 “@0” 和 “@1” 进行相加的表达式。
通过将词法分析得到的 token 数组解析并构建抽象语法树,我们可以进一步对表达式进行语义分析和求值等操作。
- current_token代表第一个token,必须要以下面三个类型开头(InputNumber、Add、Mul)","、”(" “)“不能为开头
- current_token 为 InputNumber的情况,直接返回一个叶子节点
- current_token 为 mul或者add的情况 需要进行下一层递归构建对应的左子节点和右子节点(具体规则看代码)
流程解析
按照add(@0, @1)的流程进行解析。
- 词法解析,将
add、(、@0、,、@1、)构建成为一个单词(Token)数组
- 表达式传入语法解析模块,按照语法解析的规则构建
抽象语法树。
对语法树表达式的转化:逆波兰式
例子:
add(@0, @1),逆波兰式为:@0, @1, add
做法很简单,其实就是对原有的二叉树进行后续遍历,再将括号消除即可。这样的计算顺序更加直观,并且再遇到计算(add、mul)时可以立即进行运算,因为需要的输入数已经准备好了。
两个输入操作数 && 三个输入操作数


表达式层的计算,其实就是用了一个经典的栈结构的计算,遇到输入数就压入栈中,遇到操作数就将前面的输入数出栈进行计算,将得到的结果再次压入栈中。循环下去,直到结束。
课程作业:
-
词法解析和语法解析支持sin(三角函数)操作
-
对于sin(@1),单输入如何适应,保证输出结果的正确性
具体见source/parser/parse_expression.cpp,source/layer/details/expression.cpp、include/data/tensor_util.hpp和source/tensor_utils.cpp的修改,已经通过homework的测试以及原有的测试(保证原有功能的正确性)。
需要特别注意的是在进行forward逻辑修改的时候,需要单独考虑sin(@1)的逻辑,不要和add,mul一起考虑。如果遇到sin就单独做一次出栈,sin之后再入栈,跳过剩下的部分,重新进行处理逻辑!
最后修改于 2023-09-01

本作品采用
知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。


















