中科大CUDA编程

参考资料：

• CUDA C Programming Guide，中文翻译见here
• CUDA C++ Best Practice Guide

CPU体系架构概述

现代CPU架构和性能优化

CPU是执行指令和处理数据的器件，能完成基本的逻辑和算术指令。

指令

Example：

算术：add r3,r4 -> r4

访存：load [r4] -> r7

控制：jz end

对于一个编译好的程序，最优化目标： $$ \frac{cycle}{instruction}\times \frac{seconds}{cycle} $$ 总结来说，CPI（每条指令的时钟数）& 时钟周期，注意这两个指标并不独立。

摩尔定律

芯片的集成密度每两年翻一番，成本下降一半。

CPU的处理流程

取址 -> 解码 -> 执行 -> 访存 -> 写回

流水线

使用一个洗衣服的例子，单件衣服总时间 = wash（30min）+ dry（40min）+ fold（20min）

那么洗4件衣服需要的总时间 = 30 + 40 + 40 + 40 + 40 + 20 = 210min

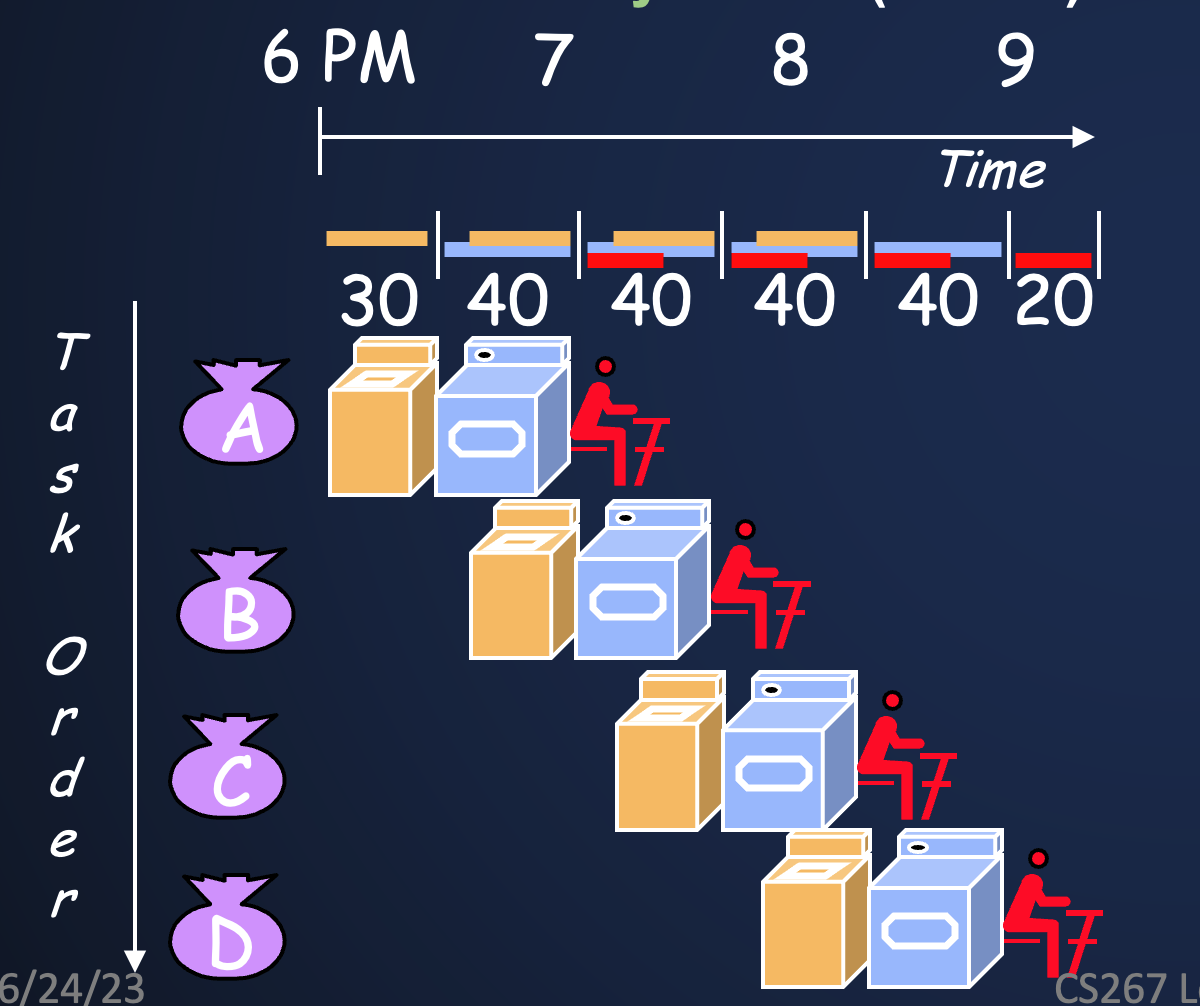
• 流水线使用的是指令级的并行，可以有效地减少时钟周期
• 增加了延迟和芯片面积（需要更多的存储）
• 带来了一些问题：具有依赖关系的指令处理，分支如何处理

旁路（Bypassing）

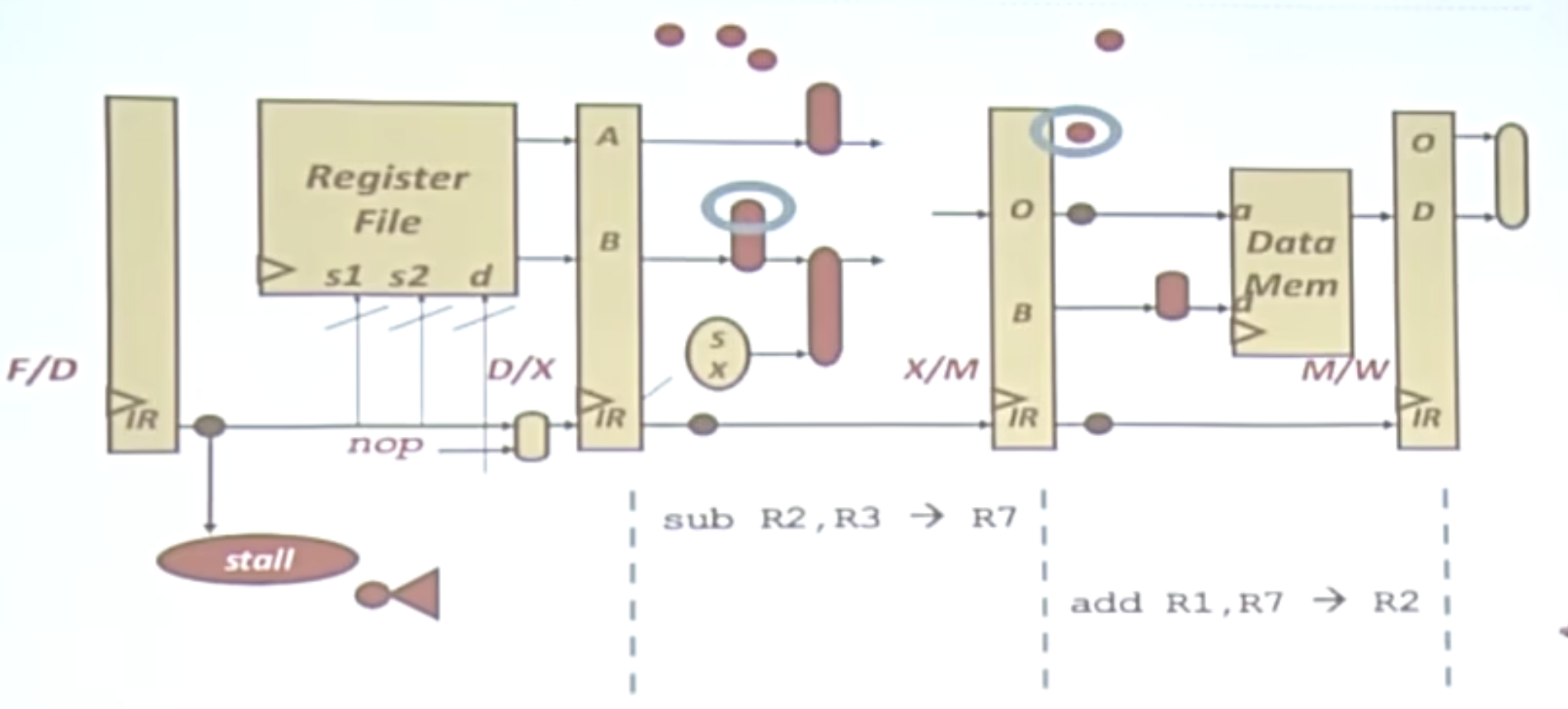
这里的两条指令具有依赖性，按照原来的方式，需要先计算R7的结果，再进行写回，访寸取到R7的结果。有了旁路这一功能，便可以跳过这个阶段，直接取到R7的结果。

流水线的停滞

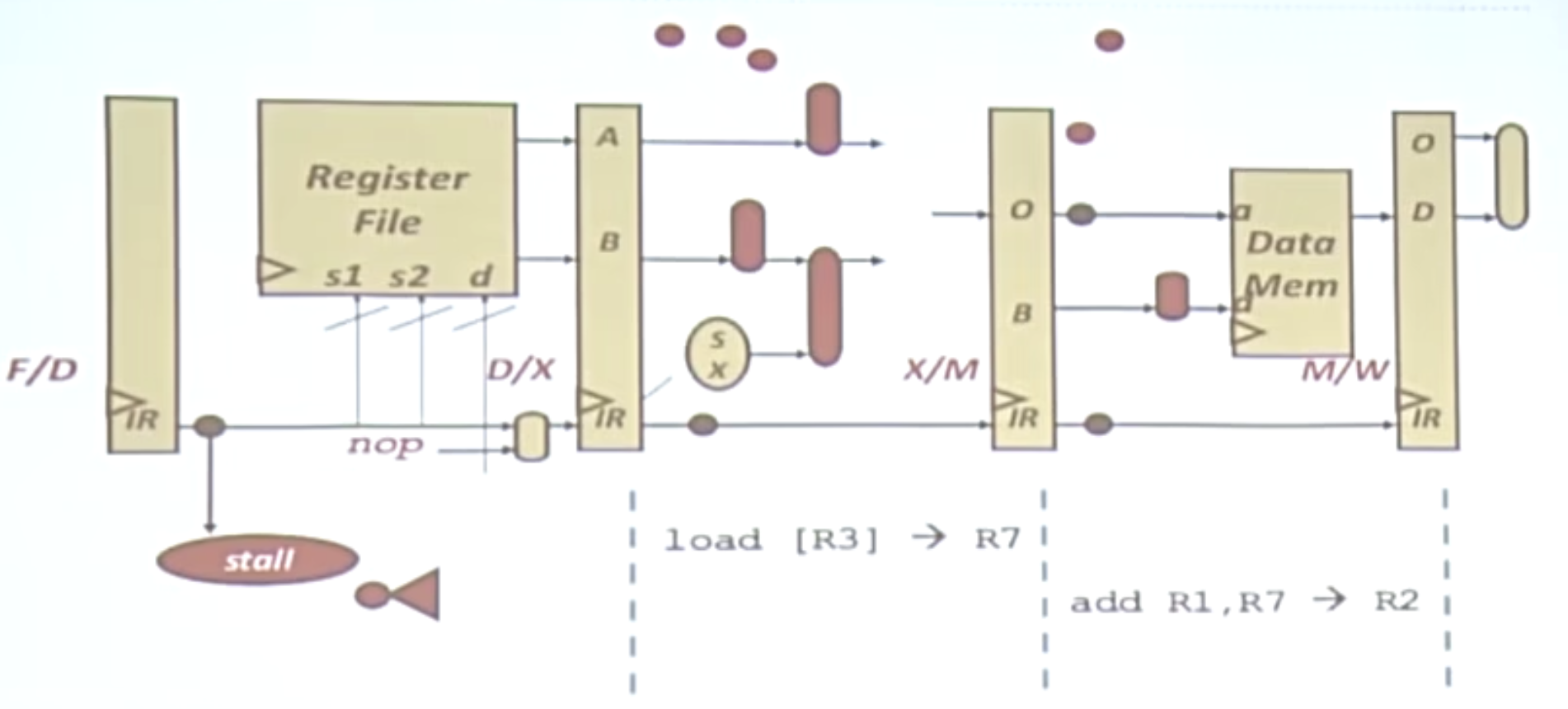
如果前面的load[R3]没有做完，流水线便会停滞。

分支

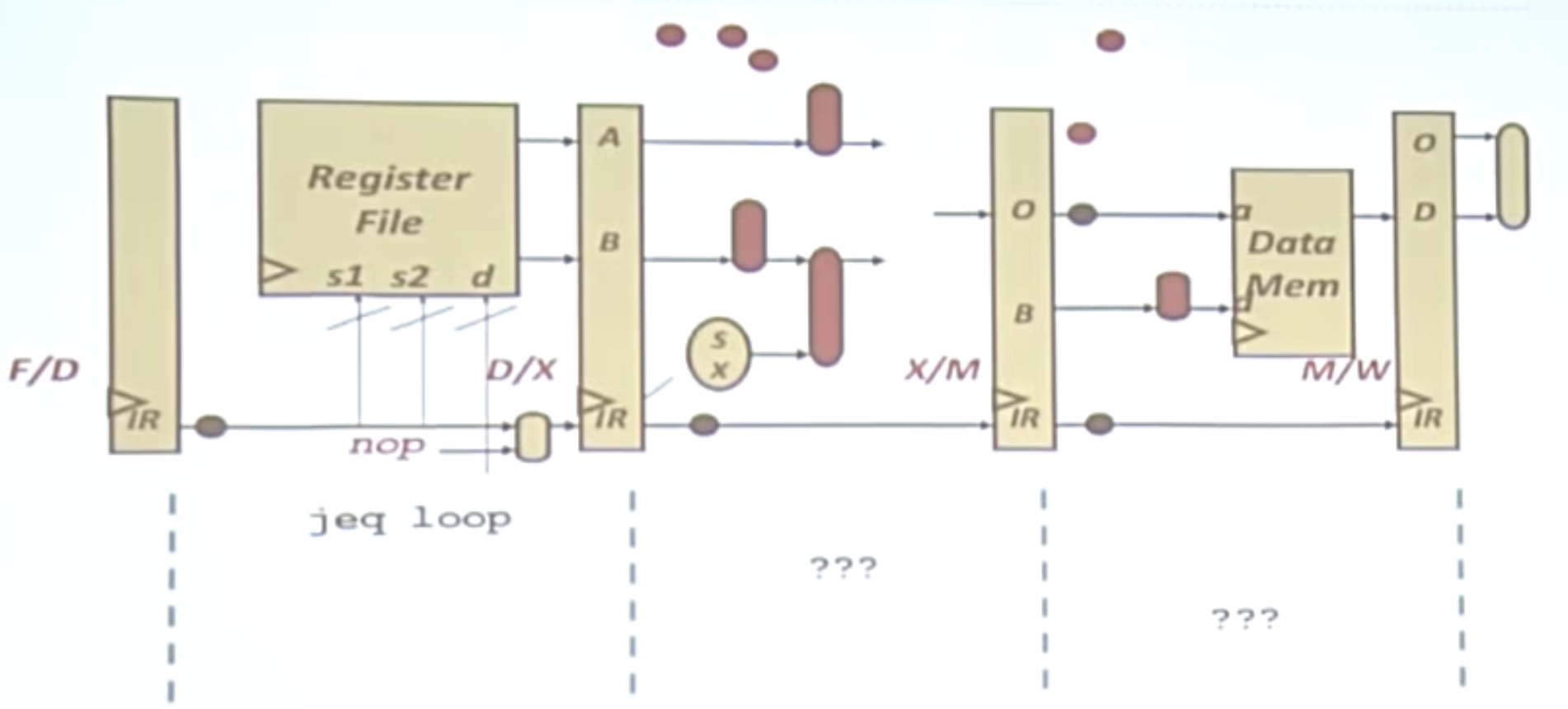
判断是否做循环jeq loop，我们并不知道是否要执行这个循环，计算机会通过分支预测等工作来进行处理。

具体的分支预测基于过去的分支记录，现代计算机的预测器准确率大于90%。同样它同样会增加芯片面积，增加延迟（预测的开销）。

分支断定

与分支预测不相同的是，它不再使用分支预测器，而是将所有分支都做一遍。

好处：不需要复杂的预测器，减少了芯片面积，减少了错误预测，在GPU中使用了分支断定。

增加CPU一个时钟周期能处理的指令数（IPC）

超标量——增加流水线的宽度，一个时钟周期处理多条指令。（超标量流水线将每个阶段细分为更小的微操作，并在多个功能单元上同时执行这些微操作。这样，多条指令可以在同一时钟周期内同时执行，从而提高处理器的吞吐量。）

这需要更多的寄存器和存储器带宽。

指令调度

考虑以下指令：

1
2
3
4

xor r1,r2 -> r3
add r3,r4 -> r4
sub r5,r3 -> r3
addi r3,1 -> r1 //addi代表减法

• xor和add是相互依赖的（读后写）
• sub和addi相互依赖（读后写）
• xor和sub不依赖（写后写）

为了让程序运行地更快，可以使用替换寄存器的方法：

1
2
3
4

xor p1,p2 -> p3
add p6,p4 -> p7
sub p5,p2 -> p8
addi p8,1 -> p9 //addi代表减法

这样我们的xor和sub就可以并行执行了。

乱序执行

将所有的指令重排，使其顺序更合理。

• 重排缓冲区
• 发射队列/调度器

存储器架构/层次

存储器越大越慢。

缓存

利用时间临近性和空间临近性，可以使我们的处理变得更快。计算机一般有3级缓存，缓存的大小越来越大。

向量运算

1
2
3

for (int i = 0; i < N; i++) {
  	A[i] = B[i] + C[i];
}

可以使用单指令多数据(SIMD)进行加速。

1
2
3
4
5
6
7

for (int i = 0; i < N; i += 4) {
  	//并行同时计算	
  	A[i] = B[i] + C[i];
  	A[i + 1] = B[i + 1] + C[i + 1];
  	A[i + 2] = B[i + 2] + C[i + 2];
  	A[i + 3] = B[i + 3] + C[i + 3];
}

x86的向量运算

• SSE：4宽度浮点和整数指令
• AVX：8宽度浮点和整数指令

线程级的并行

线程的组成：私有的寄存器、程序计数器、栈等。

程序员可以创建和线程，OS和程序员都可以对线程进行调度。

CPU的瓶颈

因为功耗墙的存在，处理器的单核性能的提升会越来越少，所以需要多核来支撑。

新摩尔定律

• 处理器越来越胖，核越来越多
• 单核的性能不会大幅提升

由此也带来了另外一堵墙，叫存储器墙，处理器的存储器带宽无法满足处理能力的提升。

并行程序设计概述

并行计算模式

并行计算是同时应用多个计算资源解决一个计算问题：

• 涉及多个计算资源或处理器
• 问题被分解为多个离散的部分，可以同时处理（并行）
• 每个部分可以由一系列指令完成

Flynn矩阵

在并行计算中，SIMD是一种很常见的方式。

常见名词

• Task：任务
• Parallel Task：并行任务，该任务可以由多个并行计算的方式解决的单个任务。
• Serial Execution：串行执行
• Parallel Execution：并行执行
• Shared Memory：共享存储
• Distributed Memory：分布式存储
• Communications：通信
• Synchronization：同步
• Granularity：粒度
• Observed Speedup：加速比，对比Baseline，并行计算能获得的性能提升。
• Parallel Overhead：并行开销
• Scalability：可扩展性

存储器架构

• 共享存储
• 分布式存储
• 分布式共享存储

并行编程模型

• 共享存储模型
• 线程模型
• 消息传递模型
• 数据并行模型

具体实例：OpenMP，MPI，Single Program Multiple Data(SPMD)，Multiple Program Multiple Data(MPMD)。

Amadahl’s Law

Amadahl’s Law的程序可能的加速比取决于可以被并行化的部分。 $$ \text{speedup} = \frac{1}{1-p}\ p代表可以被并行化的部分\ \text{speedup} = \frac{1}{\frac{P}{N} + S}\ P代表并行部分，N代表处理器数，S代表串行部分。 $$

CUDA开发环境搭建和工具配置

由于该教程是14年的教程，环境配置和如今已经完全不同，这部分将会在我的博客上呈现。

GPU体系架构概述

GPU架构

GPU是一个异构的多处理器芯片，为图形图像处理进行优化。

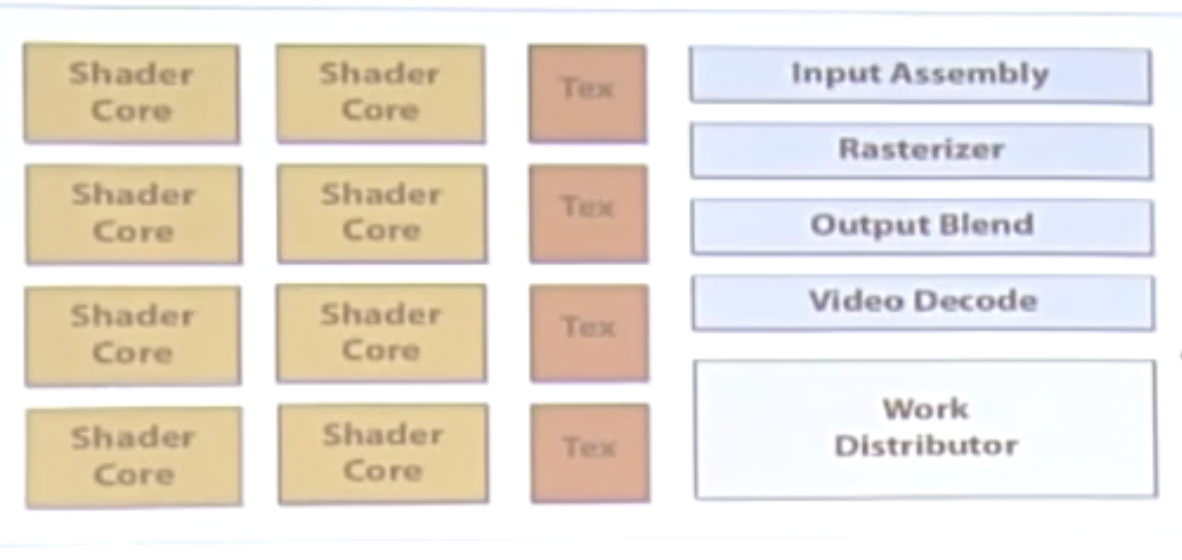
Shader core代表渲染器的核心，其组成是一个基本的ALU计算单元。

将GPU的执行单元拎出来，其结构如下：

从上到下分别是地址译码单元、计算核心、执行上下文。

现代的GPU中的ALU都共享指令集，那么为了提高效率，我们一般就通过增大ALU和SIMD来增进并行性，方便向量化的操作。

GTX480的单个架构的SM（流多处理器），一个流多处理器包含32个CUDA核心（CUDA核心本质为一个ALU）：

整个GTX480显卡可以同时承载23000个CUDA片元（也叫CUDA线程）。

GPU的存储架构

CPU存储架构

GPU的存储架构

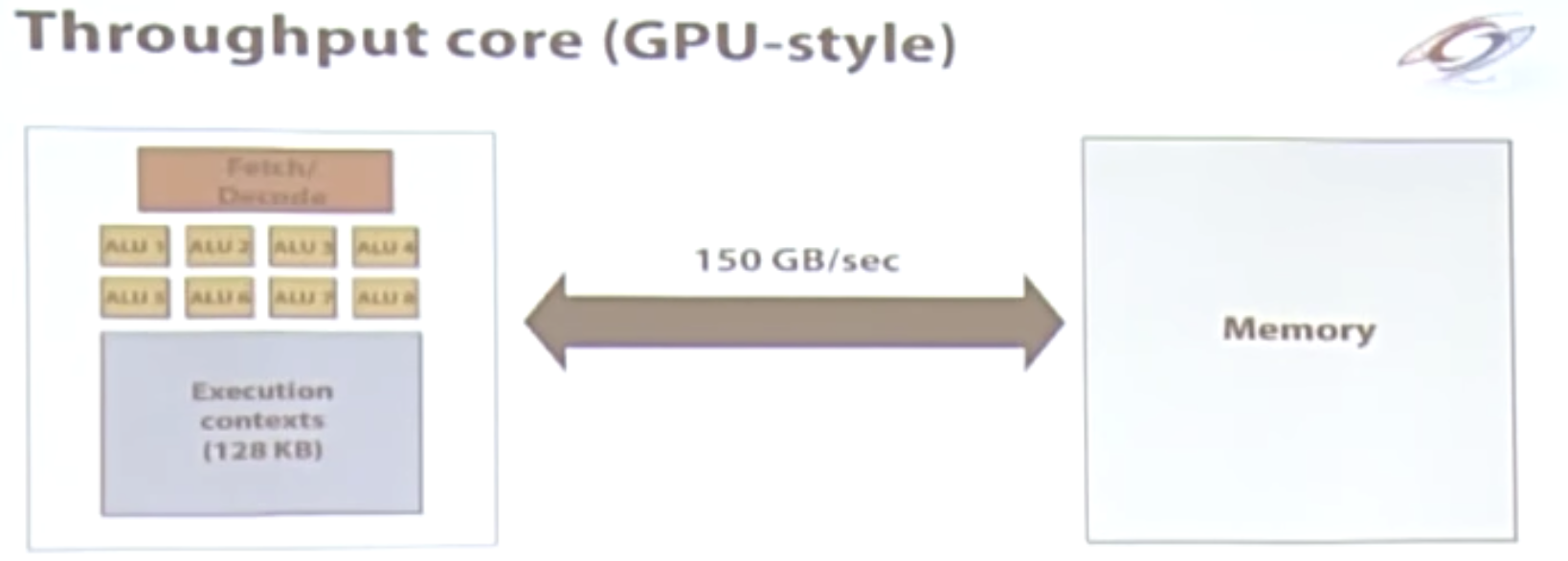
GPU的存储是交给了专门的较大的存储，显存，带宽可以达到150GB/s。访存的带宽资源是非常宝贵的资源！

看一个带宽测试的例子

$$ A、B、C为三个矩阵。\ 计算 D = A\times B + C $$

上述计算需要5个步骤：

1.Load input A[i]

2.Load input B[i]

3.Load input C[i]

4.计算A[i] * B[i] + C[i]

5.存储结果到D [i]中

如果这时候的矩阵是非常大的矩阵，那么上述几个步骤，最大的开销则发生在前3步，那么计算的效率是非常低的，这里的瓶颈是带宽。

现代的GPU通过缓存来缓解带宽受限的情况：

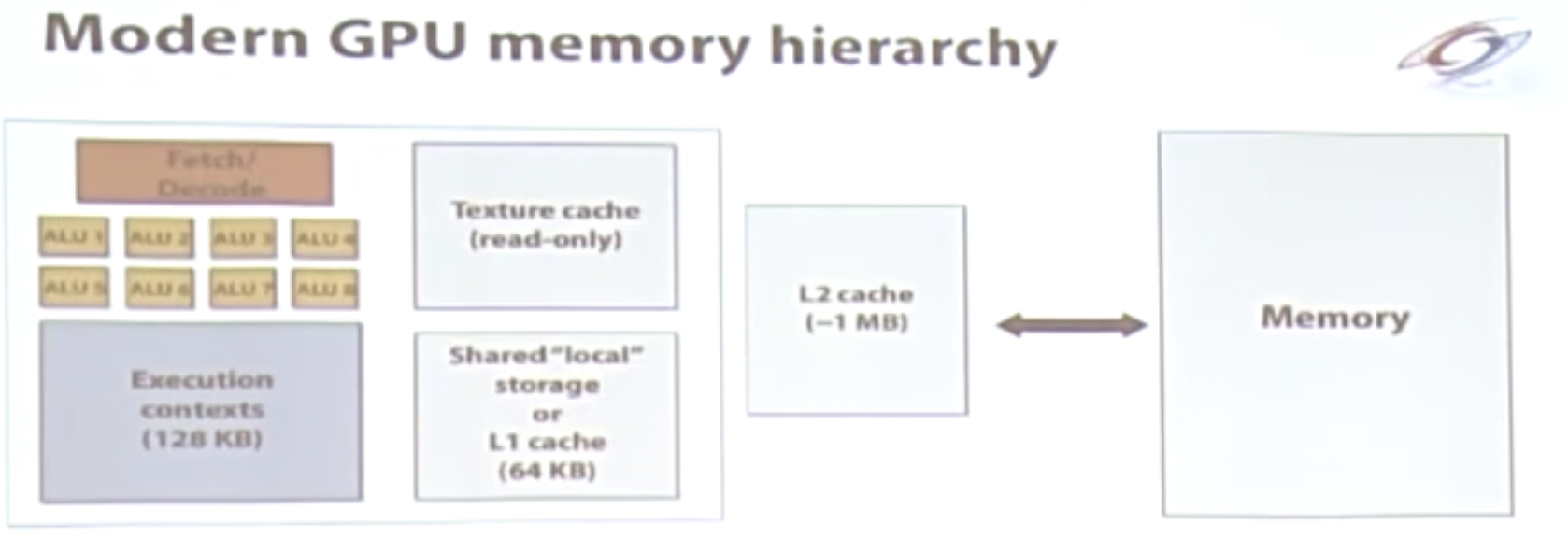
总结一下GPU是异构、众核的处理器，针对吞吐优化。

高效的GPU任务具备的条件

• 具有成千上万的独立工作
  • 尽量利用大量的ALU计算单元
  • 大量的片元（CUDA thread）切换掩藏延迟
• 可以共享指令流
  • 适用于SIMD处理
• 最好是计算密集的任务
  • 通信和计算开销比例合适
  • 不要受制于访存带宽

CUDA/GPU编程模型

CPU和GPU互动模型

cpu和gpu的交互

• cpu和gpu有各自的物理内存空间
• 它们之间通过PCIE总线相连（8G/s～16G/s）
• 交互的开销较大

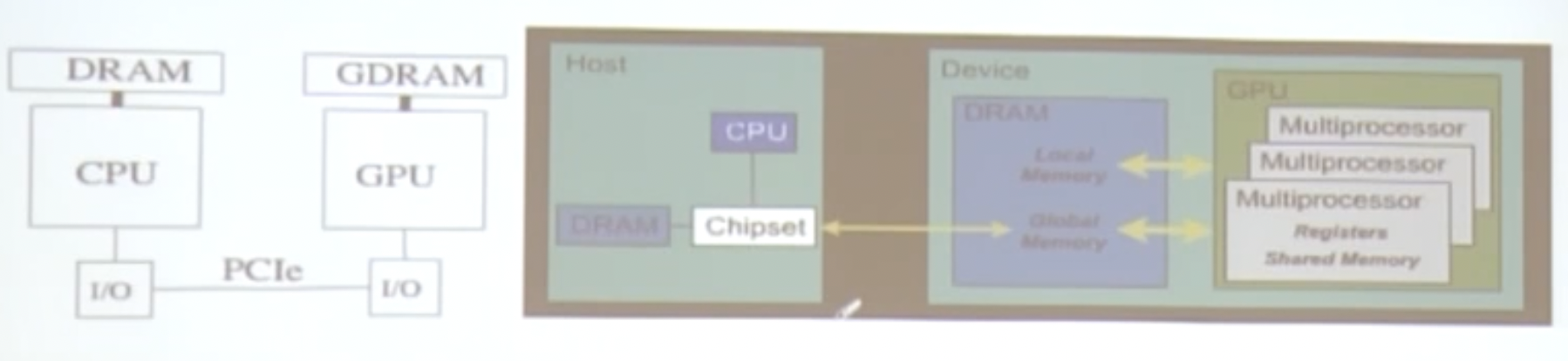
gpu的存储架构


访存速度的高低

从高到低，DRAM代表物理位置在显存中：

• Register（寄存器）- 延迟约为1个时钟周期
• Shared Memory（共享存储）- 延迟约为1个时钟周期
• Local Memory（DRAM）- 在每一个私有的线程装配的一个memory，如果寄存器放不下则装入这里，（在物理上放在显存中）速度相对较慢。
• Global Memory（DRAM）- 真正的显存，速度相对较慢
• Constant Memory（DRAM）- 相对Global和Local更慢
• Texture Memory（DRAM）- 相对Global和Local更慢
• Instruction Memory（invisible， DRAM）

GPU的线程组织模型

GPU的线程模型主要就是网格、块、线程，如下图：


注意上述示意图为软件逻辑上的组织，并不代表硬件层次。

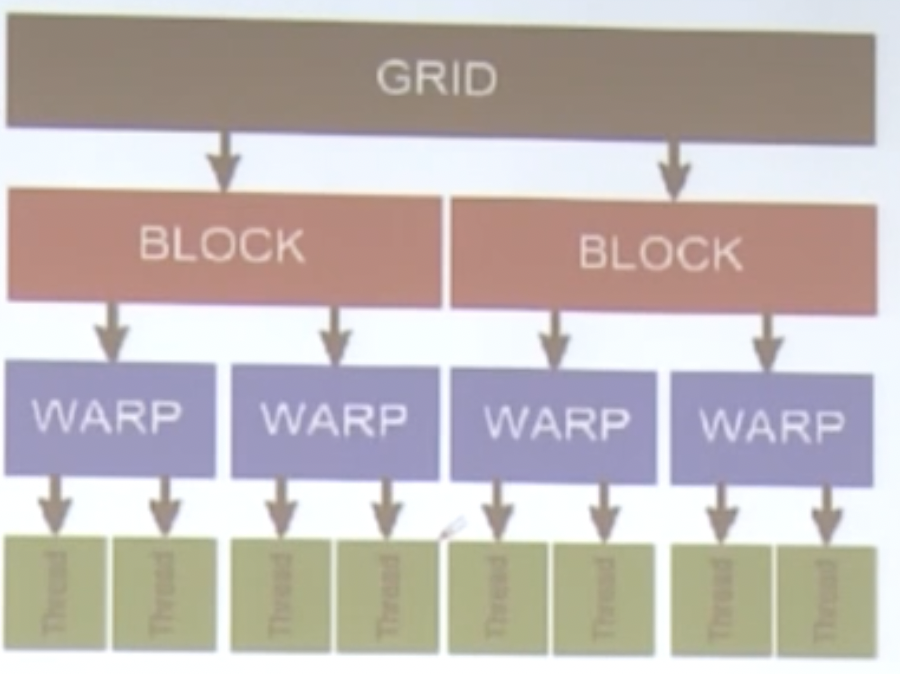
WARP代表线程束，是一些线程的组成，一般由32个连续的线程组成。

一个Kernel（通常是在GPU上执行的单个程序）具有大量的线程，这些线程被划分为多个线程块（Blocks），一个Block内部共享Shared Memory，这些Block可以进行同步。

线程和线程块具有唯一的标识。

GPU存储模型

gpu内存和线程的关系

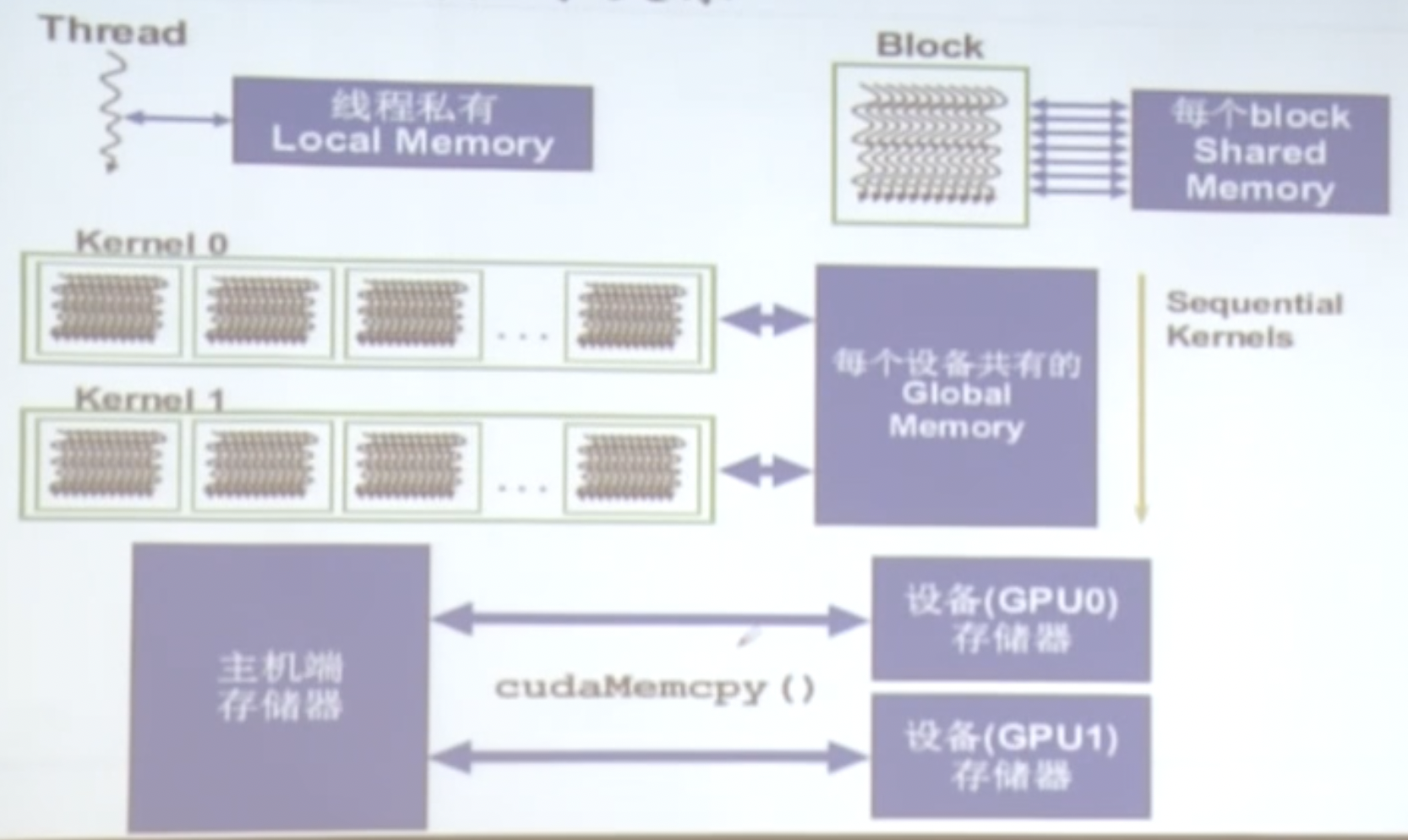
• 每个线程有一个私有的Local Memory
• 每个Block有多个线程，它们共享Shared Memory
• 整个设备拥有一个Global Memory
• 主机端的存储器可以跟不同的设备进行交互

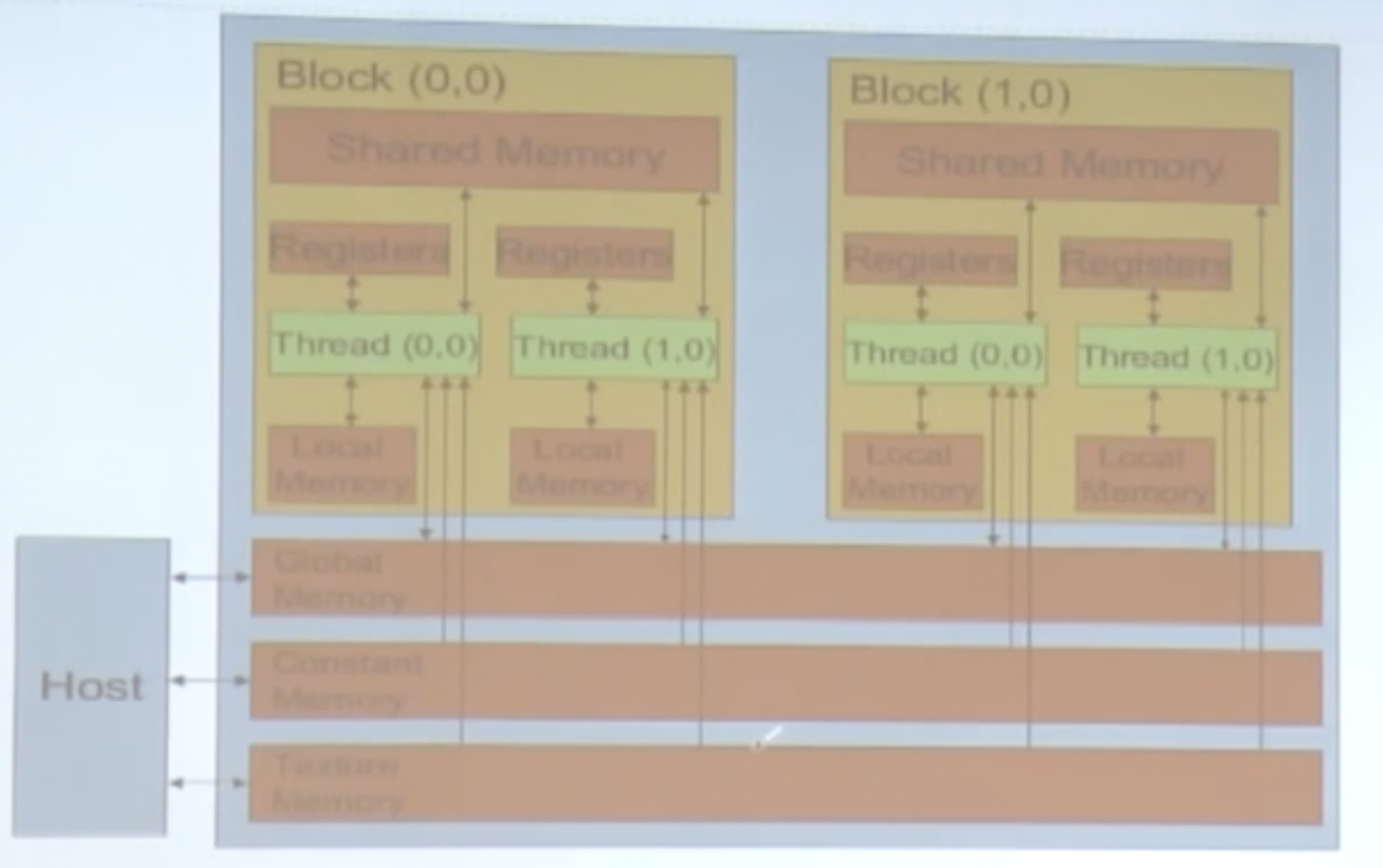
上图代表了GPU端Block内部的访问流程。

编程模型

常规的GPU用于处理图形图像，操作于像素，每个像素的操作都类似，可以应用SIMD（单指令多数据）。

SIMD可以认为是数据并行的分割：

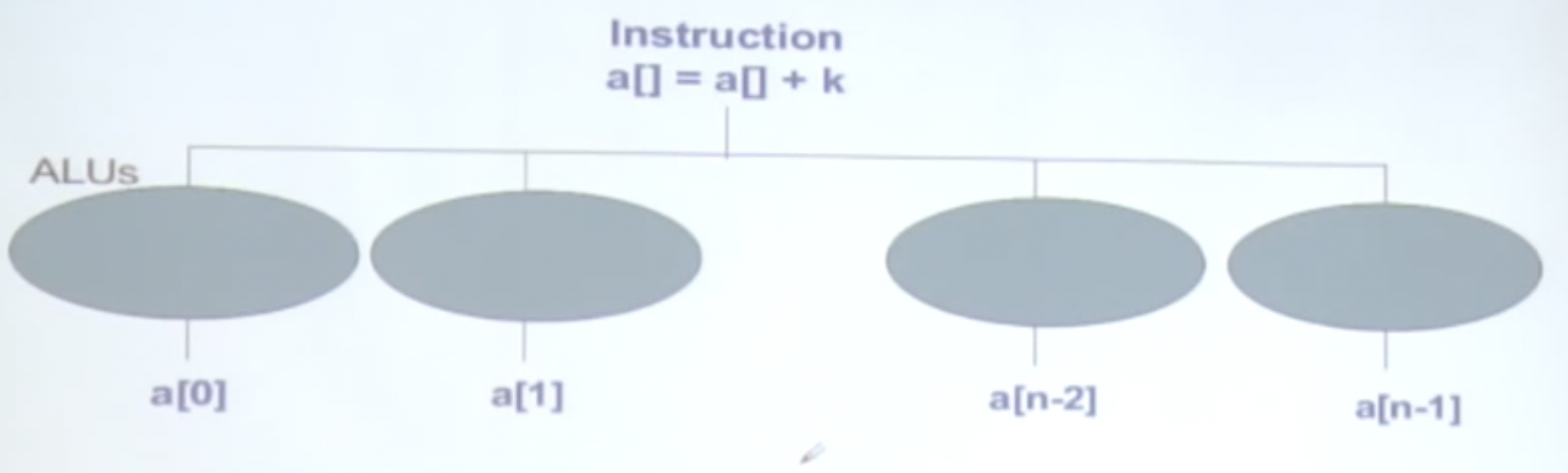
在GPU中，它被称为是SIMT：

通过大量的线程模型获得高度并行，线程切换获得延迟掩藏，多个线程执行相同的指令流，GPU上大量线程承载和调度。

CUDA编程模式：Extended C

• 修饰词：global，device，shared，local，constant
• 关键词：threadIdx，blockIdx
• Intrinsics：__syncthreads
• 运行期API：Memory，symbol，execution，management
• 函数调用：例子convolve<<<100, 10>>> (参数)

CUDA函数声明

几个需要理解的点：

• 入口函数，CPU上调用，GPU上执行
• 必须返回void
• __device__ 和__host__可以同时使用

CUDA编程（1）

CUDA术语

• Host：主机端，通常指cpu
• Device：设备端，通常指gpu
• Host和Device有各自的存储器
• Kernel：数据并行处理函数，也就是所谓的核函数，类似于OpenGL的shader
• Grid：一维或多维线程块
• Block：一组线程

一个Grid的的每个Block的线程数都是一样的，Block内部的每个线程可以进行同步，并访问共享存储器。

线程的层次

一个Block可以是一维，二维，甚至是三维的。（例如，索引数组、矩阵、体）

• 一维Block：Thread ID == Thread Index
• 二维Block：（Dx，Dy）

Thread ID of index(x, y) == x + y Dx

• 三维Block：（Dx，Dy，Dz）

Thread ID of index(x, y, z) == x + y Dx + z Dx Dy

看一个代码的例子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

__global__ void MatAdd(float A[N][N], float B[N][N],
                       float C[N][N]) 
{
  	int i = threadIdx.x;
  	int j = threadIdx.y;
  	C[i][j] = A[i][j] + B[i][j];
}

int main() {
  	int numBlocks = 1;
  	// 对于dim3的类型，如果第三个参数不传，默认为1，这样就变成了一个二维的Block
  	dim3 threadsPerBlock(N, N);
  	//第一个参数代表1个 Thread Block，第二个参数代表一个2D的Block（相当于排列的时候变成了行和列）
  	MatAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
}

一个线程块里的线程位于相同的处理器核，共享所在核的存储器。

• 块索引：blockIdx
• 块的线程数：blockDim（一维，二维，三维）

使用多个Block进行矩阵的Add：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

__global__ void MatAdd(float A[N][N], float B[N][N],
                       float C[N][N]) 
{
		int i = blockIdx.x * blockDim.x + threadIdx.x;
  	int j = blockIdx.y * blockDim.y + threadIdx.y;
  	if (i < N && j << N) {
      	C[i][j] = A[i][j] + B[i][j];
    }
}

int main() {
  	dim3 threadsPerBlock(16, 16);
  	dim3 numBlocks(N / threadsPerBlock.x , N / threadsPerBlock.y);
  	MatAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
}

线程层次结合gpu存储层次加深对代码操作的硬件理解

• Device Code：

– 读写每个线程的的寄存器

– 读写每个线程的local memory

– 读写每个线程块的shared memory（线程块内线程共享）

– 读写每个grid的global memory（不同线程块的所有线程共享）

– 只读每个grid的constant memory（每个grid的步态变化的独立空间）

• Host Code：

– 主机端只能读写global和constant memory，global memory代表全局的存储器，constant memory代表常量的存储器。

CUDA内存传输

• cudaMalloc()：在设备端分配global memory
• cudaFree()：释放存储空间

分配的代码示例：

1
2
3
4
5
6

float *Md;
int size = Widch * Width * sizeof(float);
//当前指针是指向设备上的存储空间
cudaMalloc((void**)&Md, size);
...
cudaFree(Md);

• cudaMemcpy()：内存传输，Host->Host, Host->Devicel, Device->Device, Device->Host

示例程序：

1
2
3

// Md和Pd都是在device端的地址
cudaMemcpy(Md, M, size, cudaMemcpyHostToDevice);
cudaMemcpy(P, Pd, size, cudaMemcpyDeviceToHost);

矩阵相乘

• CPU实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

void MatrixMultOnHost(float *M, float* N, flaot *P, int width) {
  //i, j分别代表行和列，k代表当前进行计算的第一个矩阵行和第二个矩阵列的位置	
  for (int i = 0; i < width; i++) {
      	for (int j = 0; j < width; j++) {
          	float sum = 0;
          	for (int k = 0; k < width; ++k) {
              	float a = M[i * width + k];
              	float b = N[k * width + j];
              	sum += a * b;
            }
          	P[i * width + j] = sum;
        }
    }
}

• CUDA算法框架，三步走：

1
2
3

1.分配我们的内存（输入的变量和输出的结果等），并进行数据传输（Host和Device之间）
2.在GPU上进行计算
3.进行数据传输（结果），并释放相应的内存

• GPU的矩阵相乘的Kernel函数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

__global__ void MatrixMulKernel(float *Md, float *Nd, float *Pd, int Width) {
  	//2D threads
  	int tx = threadIdx.x;
  	int ty = threadIdx.y;
  
  	//每一个kernel线程计算一个输出
  	float Pvalue = 0;
  	
  	for (int k = 0; k < Width; ++k) {
      	float Md_element = Md[tx * Width + k];
      	float Nd_element = Nd[k * Width + ty];
      	Pvalue += Md_element + Nd_element;
    }
  	//写入结果矩阵
  	P[tx * Width + ty] = Pvalue;
}

上述矩阵相乘的样例特点：

1.每个线程计算结果矩阵Pd的一个元素。

2.每个线程需要读入矩阵Md的一行，读入矩阵Nd的一列，并为每对元素执行一次乘法和加法。（访存的次数和计算的次数基本接近1:1）

3.矩阵的长度受限于一个线程块允许的线程数目。

思考：在算法实现中最主要的性能问题是什么？

主要的性能问题其实存在于访问存储的开销，所以算法的速度主要取决于访存的带宽（从Global Memory读数据的速度）。

CUDA编程（2）

内置类型和函数

• __global__：主机上调用，设备上执行。返回类型必须是void。
• __device__：在设备上调用，在设备上执行。
• __host__：在主机上调用，在主机上执行。

Global和device函数

1. 尽量少用递归

2. 不要使用静态变量

3. 少用malloc

4. 小心通过指针实现的函数调用

CUDA内置的向量的数据类型

• Example：

1. char[1~4]，uchar[1~4]
2. short[1~4]，ushort[1~4]
3. int[1~4]，uint[1~4]
4. long[1~4]，ulong[1~4]
5. longlong[1~4]，ulonglong[1~4]
6. float[1~4]
7. double1，double2

• 同时适用于host和device的代码，通过函数make_<type name>构造:

1
2

int2 i2 = make_int2(1, 2); 
float4 f4 = make_float4(1.0f, 2.0f, 3.0f, 4.0f);

• 通过.x，.y，.z和.w来访问：

1
2
3

int2 i2 = make_int2(1, 2);
int x = i2.x;
int y = i2.y;

常用的数学函数

• 开根号函数：sqrt、rsqrt
• 指数函数：Exp、log
• 三角函数：sin、cos、tan、sincos
• 进/舍位函数：trunc，ceil，floor

cuda中还提供了一些内建的数学函数，比上面这些函数速度更快，但精度要低一些，适合于那种对精度要求不高，但运算速度要求比较高的场合，这些函数都以双下划线__开头：__expf、__logf、__sinf、__powf等

线程同步

块内线程可以同步

• 调用__syncthreads创建一个barrier栅栏
• 每个线程在调用点等待块内线程执行到这个地方，然后所有线程继续执行后续指令：

1
2
3

Mds[i] = Md[j];
__syncthreads();
func(Mds[i], Mds[i + 1]);

线程同步带来的问题

线程同步会带来部分线程的暂停，线程同步可能还会带来更严重的问题,死锁：

1
2
3
4
5
6

//这里的部分线程执行的时候会在上面那个分支等待，而部分线程在下面等待，永远无法同步，造成死锁
if (someFunc()) {
  	__syncthreads();
} else {
  	__syncthreads();
}

线程调度

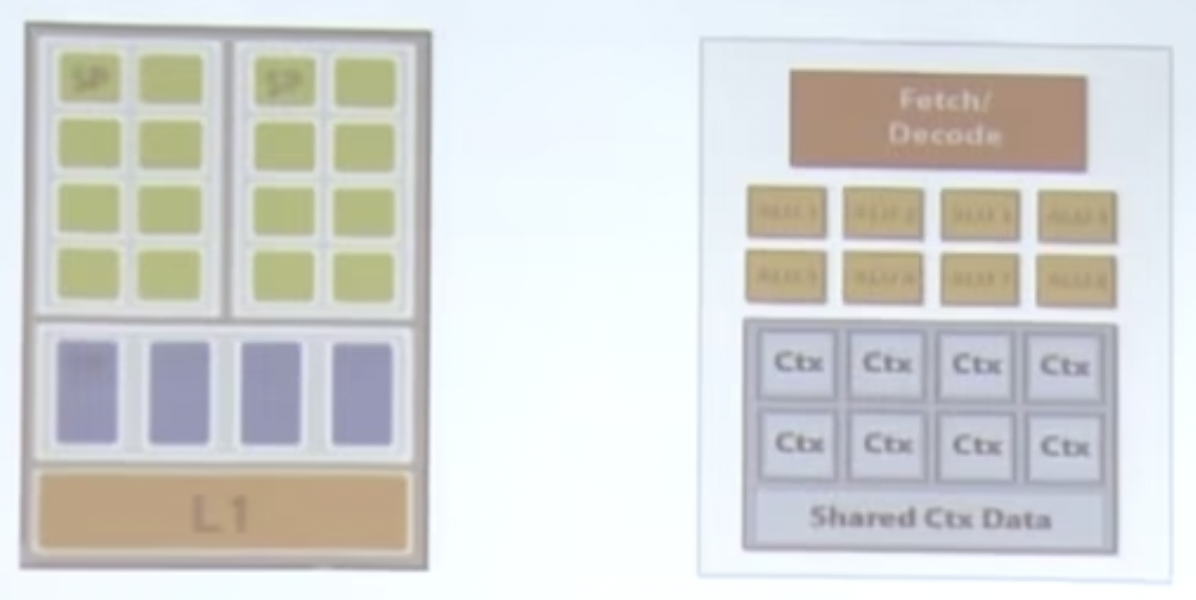
左边是一个的流多处理器（SM）的物理结构，右边为其逻辑结构。

一个绿色的小块为一个流处理器（SP），在这个GPU（古老）中，8个SP组成一个SM。

Warp：块（Block）内的一组线程

• 一个Warp有32个线程。
• 运行于同一个SM，是线程调度的基本单位。
• threadIdx值连续。
• 硬件上保证了一个Warp内的线程是天然同步的。

一个例子：

1

一个SM上，有3个Block，每一个Block被切分成了若干个warp：这时执行程序会根据warp为单位执行上下文切换等操作并进行调度。

• 在一个硬件上，warp的调度是0开销的！原因是一个warp需要的资源（上下文）在硬件结构上是不变的，只需要进行warp的切换。使用现实生活举例就是一个饭桌是固定的，只需要切换吃饭的那一伙人就OK。

• 在一个SM上，任一时刻只有一个warp在执行

如果一个warp内的线程沿着不同的分支执行会有什么后果？

这种情况为divergent warp，在不同的执行分支下，所有的warp的执行顺序是统一的，比如先执行if里面的内容，再执行else的内容。

假设一个SM中只有8个SP，那么如何给线程分配SP？

按照构想，其实也就是轮流使用的过程：warp内的32个线程按照8个线程一批的形式轮流使用SP。

存储模型

寄存器

每个SM内部的寄存器对线程来说是竞争模型。

假设一个SM内部有8000个寄存器，768个线程，那么每个线程能分配到10个寄存器。超出限制后线程数将因为block的减少而减少。

Example：每个线程用到了11个寄存器，并且每个block含256个线程，那么一个SM可以驻扎多少个线程，一个SM可以驻扎多少个warp？warp数变少了意味着什么？

768/256 = 3， 原本可以分配3个block，但是由于寄存器数量不够用，最多只能分配给512个线程。 那么线程数就会减少到512个，属于2个block，一个SM只能有512/32 = 16个。warp数量的减少意味着效率的降低，剩余的寄存器也会闲置。

局部存储器（Local Memory）

**局部存储器是存储于global memory（显存），作用域是每个thread，是线程私有的空间。**一般用于存储自动变量数组，通过常量索引访问，速度较慢。

共享存储器（Shared Memory）

其存储层次和cache是同一等级的，用户可进行编程，速度较快。

全局存储器（Global Memory）

全局存储器其实就是显存，长延时，可读写。如果是随机访问会非常影响性能，Host主机端可以读写。

常量存储器（Constant Memory）

短延时，高带宽，当所有线程访问同一位置时只读。存储于global memory但是有缓存，Host主机端可以读写，经常用于存储常量。

那么如何去声明这些变量呢？

变量的访问

• global和constant变量：

  • Host可以通过以下函数访问：

    cudaGetSymbolAddress()：找到要访问变量的地址

    cudaGetSymbolSize()：得到访问变量的大小

    cudaMemcpyToSymbol()：将数据从Host内存复制到Device内存中的一个常量符号（Symbol）位置。

    cudaMemcpyFromSymbol()：将数据从Device内存中的一个常量符号位置复制回到Host内存中

  • Constans变量必须在函数外声明

CUDA编程（3）

矩阵乘法重分析

为了去除长度的限制，一般优化的做法就是将Pd矩阵拆成tile小块，把一个tile布置到一个block上，并通过threadIdx和blockIdx索引。

修改后的代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

__global__ void MatrixMulKernel(float *Md, float *Nd, float *Pd, int width) {
  	// 注意这里的行和列与CUDA中的相反的，不相反也没有关系
		int Row = blockIdx.y * blockDim.y + threadIdx.y;
  	int Col = blockIdx.x * blockDim.x + threadIdx.x;
  	
  	float Pvalue = 0;
  	for (int k = 0; k < Width; ++k) {
      	Pvalue += Md[Row * Width + k] * Nd[k * Width + Col];
    }
  	Pd[Row * Width + Col] = Pvalue;
}

CUDA中的索引和矩阵索引是如何做的？

对于CUDA的global memory来说，没有二维数组的功能，所以行优先与列优先是无所谓。所以在GPU的Global级别编程里没有交换循环顺序带来性能提升的说法。但是在CUDA的shared memory中，默认是按照行优先来计算的。所以变换成列优先会有很大的性能提升。

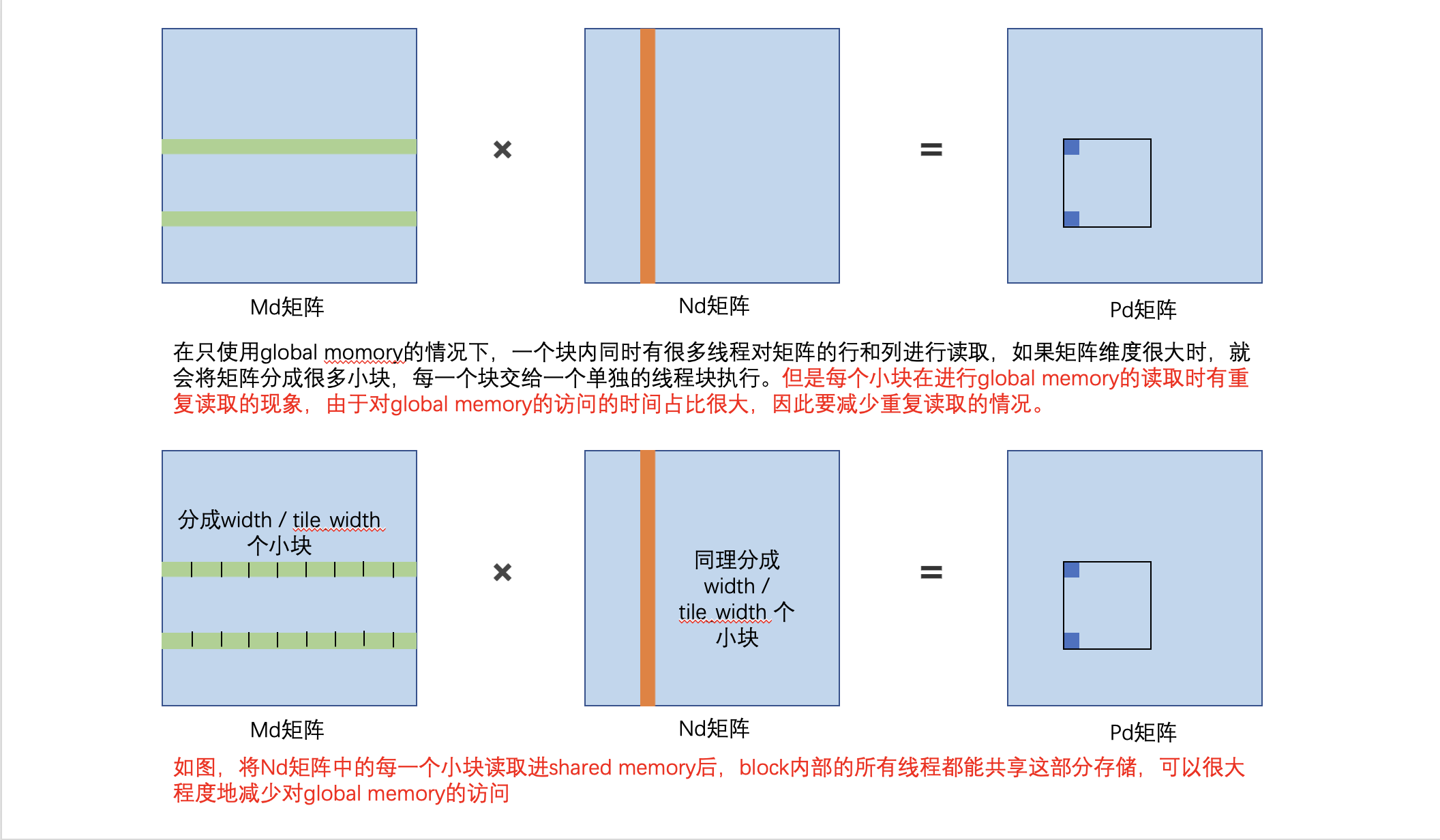
对于矩阵相乘时，Global memory的访问开销占大部分的时间，如何减少访问带来的消耗？

其实我们在做矩阵乘法的时候，有很多重复的读取：

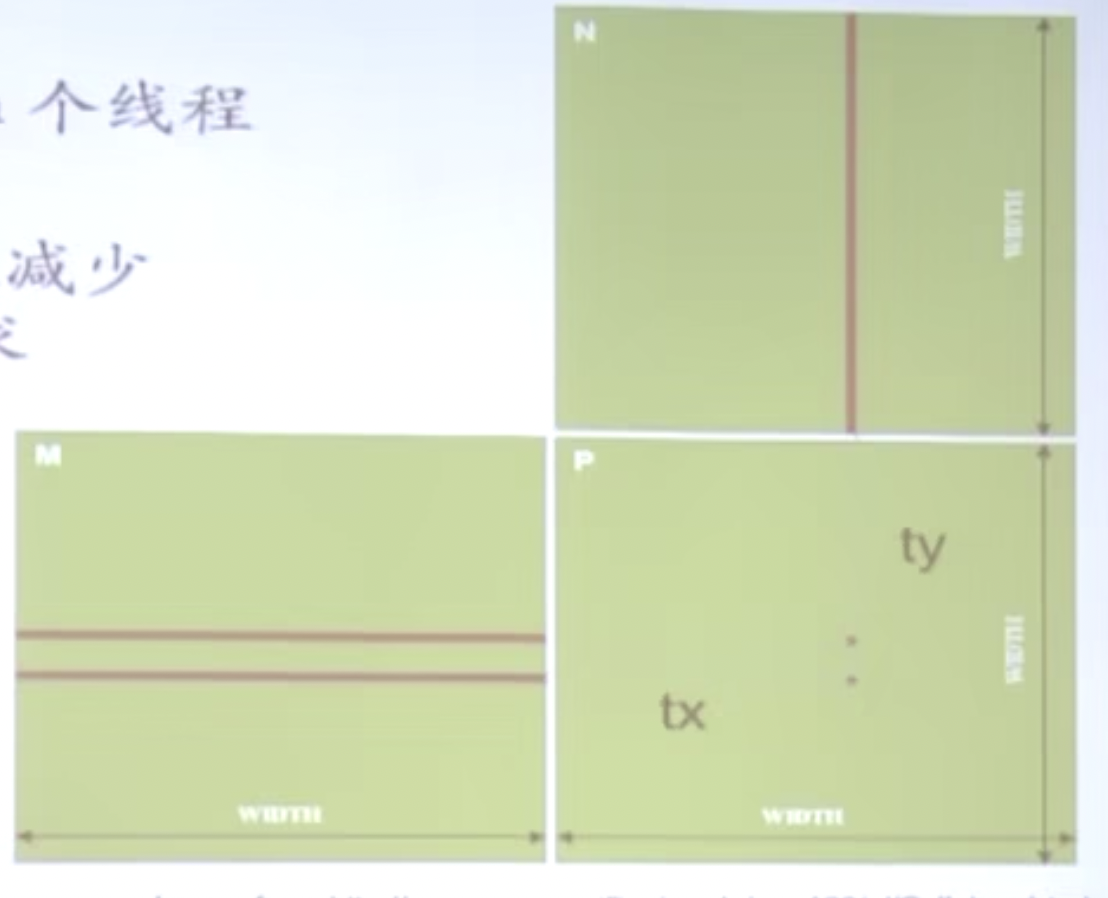
在两个位置进行计算的时候，读取的是同一列的数据，多了很多重复读取。

• 解决方法是每个输入元素被Width个线程读取，使用shared memory来减少global memory带宽需求：

将Kernel函数拆分成多个阶段，每个阶段使用Md矩阵和Nd矩阵的子集累加Pd矩阵，这样每个阶段都有很好的数据局部性。

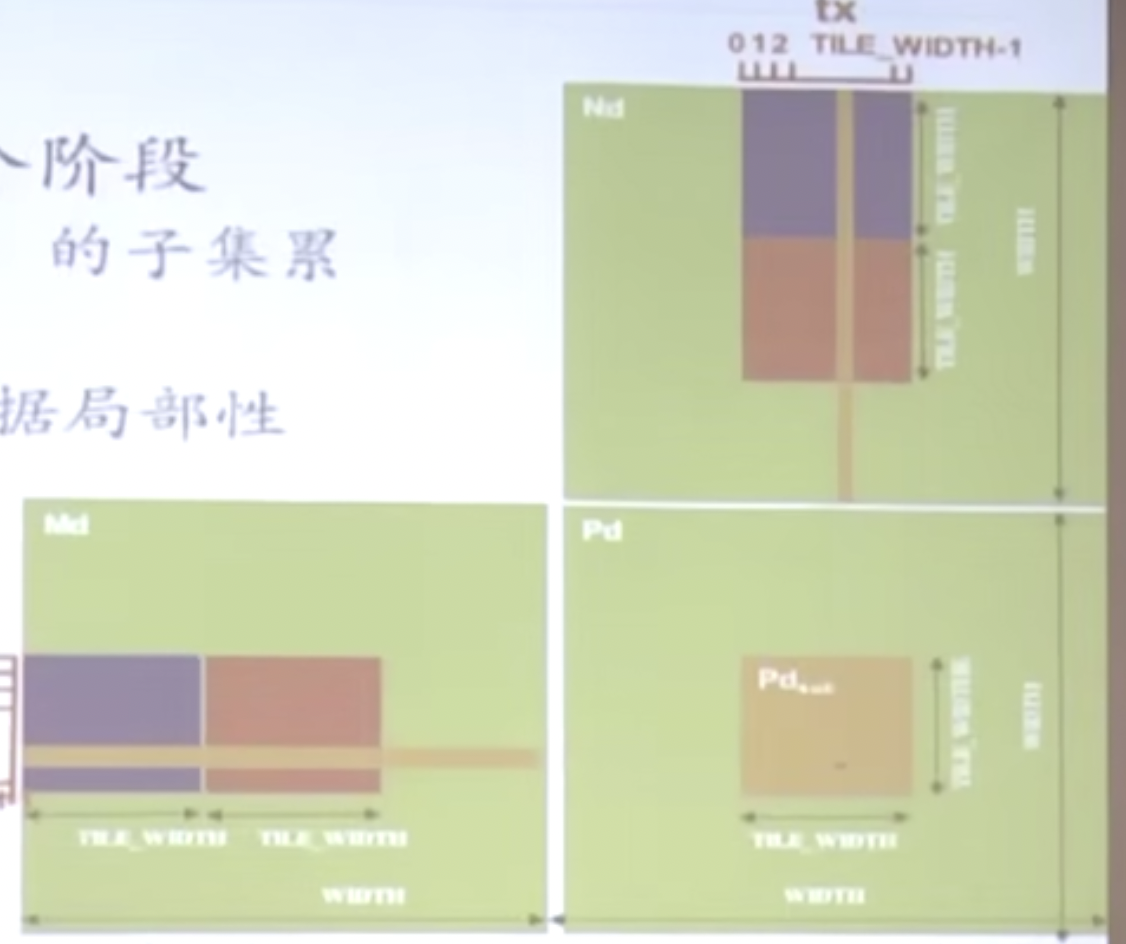
但由于shared memory的大小是有限的，我们将条块读取也需要分批读取。

代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

__global__ void MatrixMulKernel(float *Md, float *Nd, float *Pd, int width)
{
  	// 定义Shared memory存储Md和Nd的子集
  	__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
  	__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];
  	
  	int bx = blockIdx.x;
  	int by = blockIdx.y;
  	int tx = threadIdx.x;
  	int ty = threadIdx.y;
  	
  	int Row = by * TILE_WIDTH + ty;
  	int Col = bx * TILE_WIDTH + bx;
  	
  	float Pvalue = 0;
  	// 将整个矩阵的运算分成Width / TILE_WIDTH 个阶段进行 
  	for (int m = 0; m < Width / TILE_WIDTH; ++m) {
      	// 从Md和Nd中各取一个元素存入shared memory
      	// 从二维的角度来说为Md[Row][m * TILE_WIDTH + tx]，取第一个矩阵小块的行
      	// 从二维的角度来说为Nd[m * TILE_WIDTH + ty][Col]，取第二个矩阵小块的列
      	Mds[ty][tx] = Md[Row * Width + (m * TILE_WIDTH + tx)];
      	Nds[ty][tx] = Nd[Col + (m * TILE_WIDTH + ty) * Width];
      	// 等待所有block内的线程同步后才能进行乘累加
      	__synchthreads();
      	// 每一个TILE_WIDTH子集做乘累加
      	for (int k = 0; k < TILE_WIDTH; ++k) {
          	Pvalue += Mds[ty][k] + Nds[k][tx];
        }
      	// 防止上次的乘累加还没有完成，下一次从Global -> shared过程的元素对乘累加的结果造成影响
      	__synchthreads();
    }
  	Pd[Row * Width + Col] = Pvalue;
}

上述程序整体的流程：

1. 计算结果矩阵Pd中元素的row和col来确定要取Md的哪一行，哪一列。
2. 根据行列将其分为一个个小块，分别把小块放入Shared Memory
3. 在Shared Memory进行计算
4. 这里的同步体现在每一个小块上的读取是可以并行的，为O(1)。而且可以有效减少对global memory的访问次数

那么如何选取TILE_WIDTH的数值

一个块内的线程数是有上限的，TILE_WIDTH的数目不要大于BLock内部的线程数，同时Shared Memory大小是有极限的。更大的TILE_WIDTH将导致更少的Block数。

原理如图所示：

原子函数

CUDA中的原子操作本质上是让线程在某个内存单元完成读-修改-写的过程中不被其他线程打扰，它是一个独占的过程。

举个例子来说：我有很多线程，每个线程计算出了一个结果, 我需要把所有的结果加在一起，就必须使用原子操作，不然就会发生错误。因为可能会发生一个线程正在读，另一个线程正在写的过程。所以就需要一个原子加的操作过程，如下图：

• 算术运算：atomicAdd(),atomicSub(),atomicExch(),atomicExch(),atomicMin(),atomicMax(),atomicDec(),atomicCAS()
• 位运算：atomicAnd(),atomicOr,atomicXor()

这些原子函数具体的作用可以参考CUDA原子操作详解及其适用场景 - 知乎 (zhihu.com) 原子操作是比较耗时的，需要进入一个排队机制，尽量少用。

CUDA程序基本优化

有效的数据并行算法 + 针对GPU架构特性的优化 = 最优性能

Parallel Reduction：并行规约

下面是一个并行规约的过程：

也就是每两个数进行一次合并！

GPU程序如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

__global__ void parallel_reduction() {
  	__shared__ float *partialSum;
  	// Load into shared memory
  	int t = threadIdx.x;
  	for (int stride = 1; stride < blockDim.x; stride *= 2) {
      	// 同步是为了每一层的规约做完了之后才能做下一层
      	__syncthreads();
      	if (t % (2 * stride) == 0) {
          	partialSum[t] += partialSum[t + stride];
        }
    }
}

以8个数为例，每次我们启动8个线程读取，在做加法时，实际上工作的线程只有4个线程，由于同步的需求，多余的线程就闲置了。

也就是说n个元素实际上只需要n/2个线程，也就是说每轮所需要的线程数都减半！

按照上图的方式，我们可以通过改变索引来实现这个需求，那么我们stride的顺序从1，2，4变为了4，2，1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

__global__ void parallel_reduction() {
  	__shared__ float *partialSum;
  	// Load into shared memory
  	int t = threadIdx.x;
  	for (int stride = blockDim.x / 2; stride > 0; stride /= 2) {
      	// 同步是为了每一层的规约做完了之后才能做下一层
      	__syncthreads();
      	if (t < stride) {
          	partialSum[t] += partialSum[t + stride];
        }
    }
}

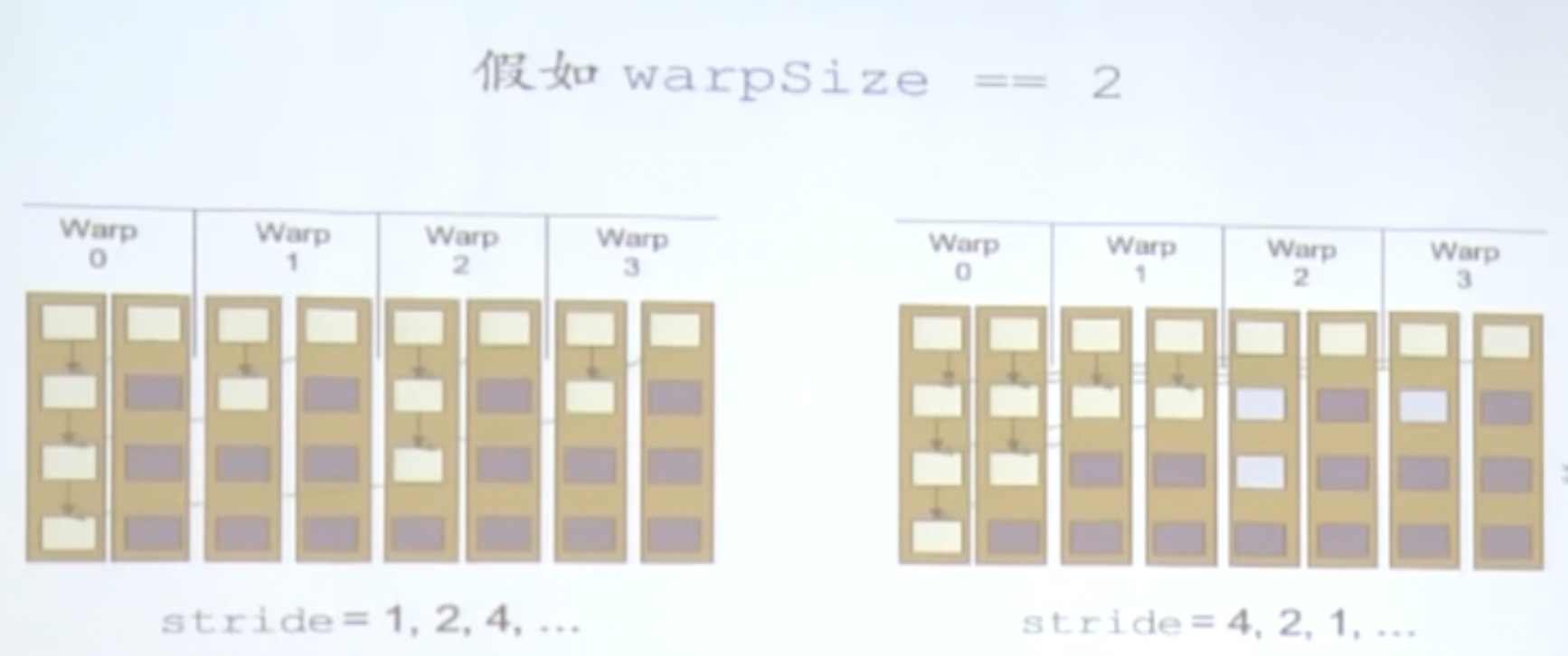
因为线程进行计算的方式进行了改变，因为warp是线程调度的基本单位，这样的排列方式可以让更多闲置的线程可以提前释放资源。

Warp分割

线程块内如何划分warp

通晓warp分割有助于减少分支发散，让warp尽早完工。

• Block被划分为以32个连续的线程组叫一个warp
• warp是最基本的调度单位
• warp一直执行相同的指令
• 每个线程只能执行自己的代码路径
• 设备切换没有时间代价

CUDA程序深入优化

访存造成的延迟

CPU-GPU数据传输最小化

• Host <--> Device的数据传输带宽远低于global momory
• 减少这种传输的方法：
  • 1.中间数据直接在GPU分配，操作，释放
  • 2.部分代码在GPU内部重复计算的开销可能比总线（pcie）传输的开销更大
  • 3.如果将CPU代码移植到GPU，但是这个中间传输的过程还在，可能无法提升性能（此时中间传输的开销大于GPU计算的开销）
• 组团传输
  • 大块传输的性能好于小块
• 内存传输与计算时间重叠
  • 双缓存解决

Memory Coalescing：访存合并

这被认为是最重要的影响因子！

GPU的Global memory的带宽虽然很高，但是延时是很高的。

带宽和延时的理解：

带宽可以比喻为高速公路上的宽度，允许多少数据同时经过；延时可以比喻为在高速公路上开车的速度。

问题：给定一个矩阵用行优先的方式存储于global memory，对一个thread来说比较适合的访存模式是什么？

如果满足访问存储合并条件（相邻的线程访问相邻的内存），一个warp的线程访问Global memory的32、64或128位宽数据，结果只需要1或者2次传输。

**Shared Memory **:

• 比global memory快上百倍
• 可以通过缓存数据减少global memory的访存次数
• 线程可以通过shared memory协作
• 用来避免不满足合并条件的访存：
  • 读入shared memory重排顺序，从而支持合并寻址。

Shared Memory架构

• 很多线程访问存储器
  • 因此存储器被划分为banks
  • 连续的32-bit访存被分配到连续的banks
• 每个bank每个周期可以响应一个地址
  • 如果有多个bank的话可以同时响应更多的地址申请
• 对同一个bank进行多个并发访存将导致bank冲突
  • 冲突的访存必须串行执行

Bank冲突

下面两种是不会发生bank冲突的内存访问方式：

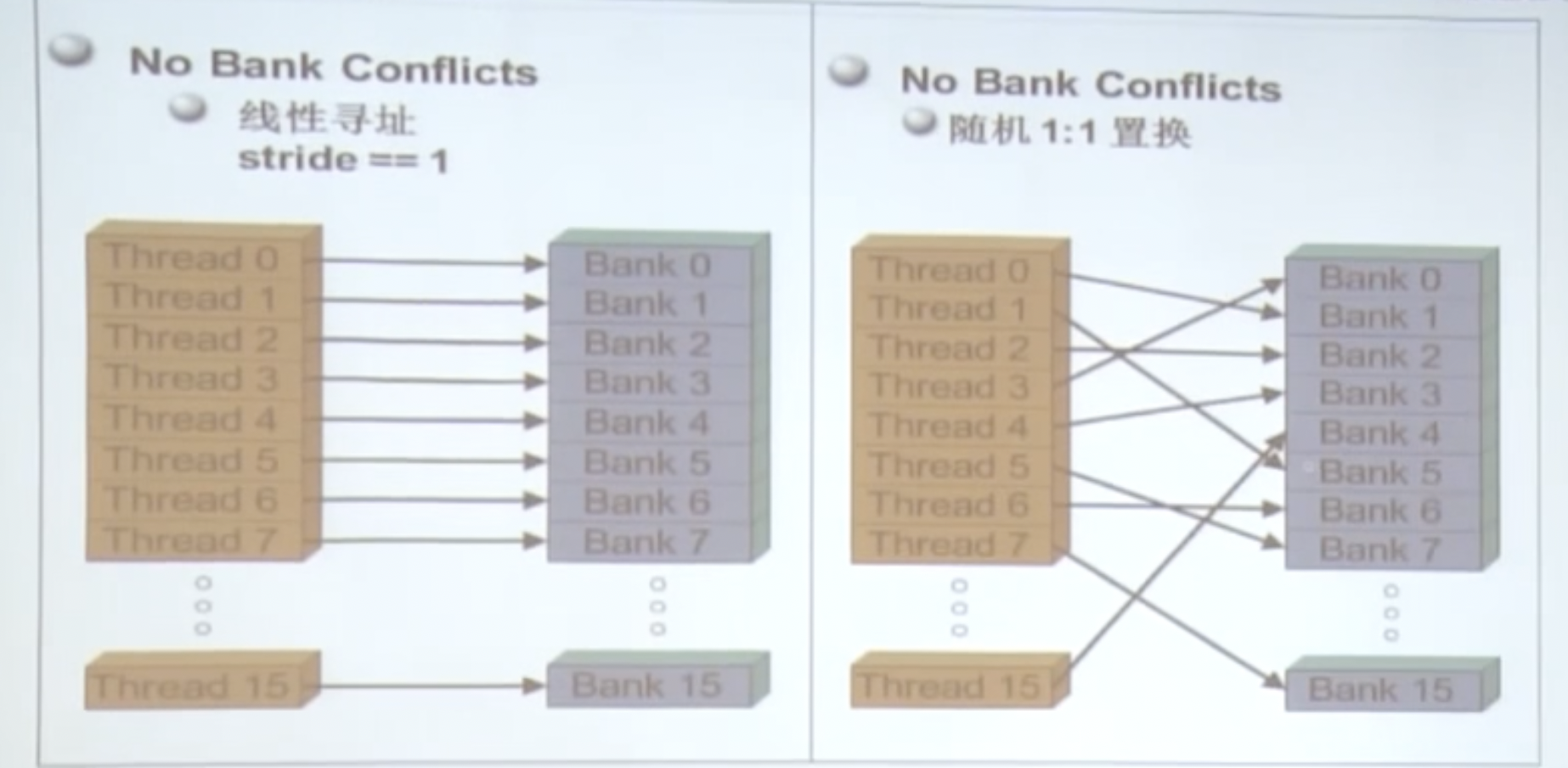
下面两种是容易发生bank冲突的内存访问方式：


一般来说，多少路的bank冲突就会导致多少倍的性能下降。

• 通常来说，没有bank冲突shared memory和registers一样快。
• warp_serialize profiler分析器的可以反映冲突
• 快速情况：
  • half-warp内所有线程访问不同的banks，没有冲突
  • half-warp内所有线程读取同一地址，没有冲突（广播）
• 慢速情况：
  • Bank Conflict：half-warp内多个线程访问同一个bank
  • 访存必须串行化
  • 代价 = 多个线程同时访问同一个bank的线程数的最大值

举例：Transpose 矩阵转置

• 每个线程块在矩阵的一个warp上操作
• 原始版本存在对global memory按步长访问的情况

原始矩阵转置：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

__global__ void transposeNaive(float *odata, float *idata, int width, int height)
{
  	int xIndex = blockIdx.x * TILE_DIM + threadIdx.x;
  	int yIndex = blockIdx.y * TILE_DIM + threadIdx.y;
  
  	int index_in = xIndex + width * yIndex; // [xIndex, yIndex]
  	int index_out = yIndex + width * xIndex; // [yIndex, xIndex]

  	odata[index_out] = idata[index_in];
}

通过shared memory实现合并

• 先将warp的多列元素存入shared memory，再以连续化的数据写入global memory
• 需要同步__syncthreads()，因为线程需要用到其他线程存储到shared memory的数据。

代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

__global__ void transposeCoalesced(float *odata, float *idata, int width, int height)
{
  	__shared__ float tile[TILE_DIM][TILE_DIM];
  	
  	// 计算原矩阵的坐标 
  	int xIndex = blockIdx.x * TILE_DIM + threadIdx.x;
  	int yIndex = blockIdx.y * TILE_DIM + threadIdx.y;
  	int index_in = xIndex * width + yIndex; // 行元素：[xIndex, yIndex]
  	
  	// 计算转置矩阵的坐标	
  	xIndex = blockIdx.y * TILE_DIM + threadIdx.y;
  	yIndex = blockIdx.x * TILE_DIM + threadIdx.x;
  	int index_out = xIndex + yIndex * height; // 列元素：[xIndex, yIndex]
  	
  	//读入shared memory [y, x] = [xIndex, yIndex]
  	tile[threadIdx.y][threadIdx.x] = idata[index_in];
  	__syncthreads(); // 同步
  	
  	// [yIndex, xIndex] = [x, y]:[xIndex, yIndex]
  	odata[index_out] = tile[threadIdx.x][threadIdx.y];
}

现在还存在一个问题：

• warp内的16$\times$16个floats存在于shared memory：
  • 列中的数据存于相同的bank
  • 读入warp – 列数据存在16路的bank conflict
• 解决方案 – 填充shared memory数组
  • __shared__ float tile[TILE_DIM][TILE_DIM + 1]
  • 反对角线上的数据存于相同的bank

使用Padding避免存储体冲突（填充数组），见下图：

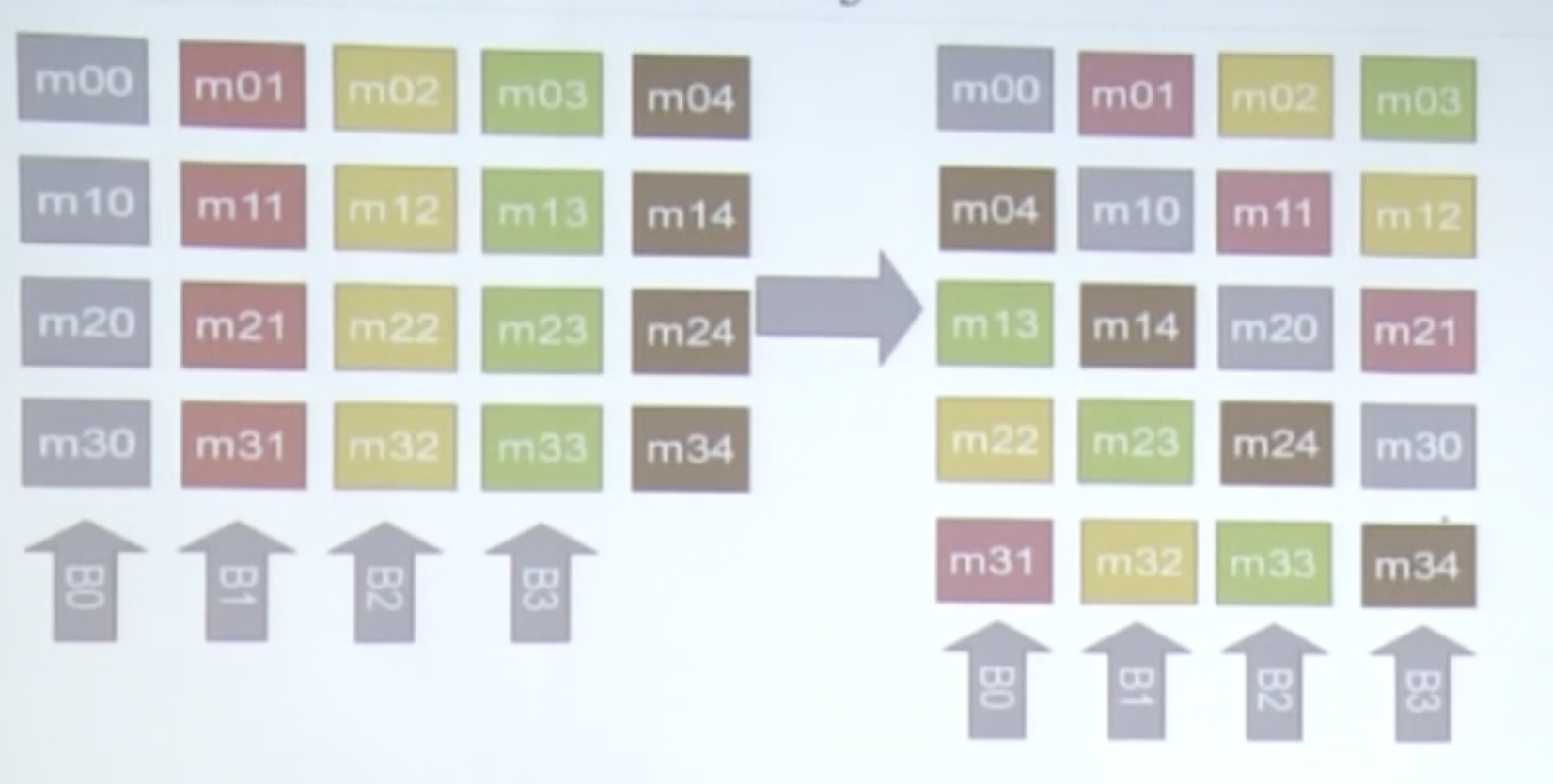
原来假设为4个bank，现在填充数组的时候多填充一位，但由于bank是按顺序读取，那么棕色的部分就会占位，但不会产生作用。所以Bank读取时不会产生冲突。

CUDA的Texture纹理

Texture是读入数据的一个对象。

优点：

• 数据被缓存：特别适用于无法合并访存的场合
• 支持过滤：线性、双线性、三线性 插值
• Wrap模式（针对越界寻址）：裁剪到边缘或重复
• 一维、二维、三维寻址：以整数或归一化小数做为坐标

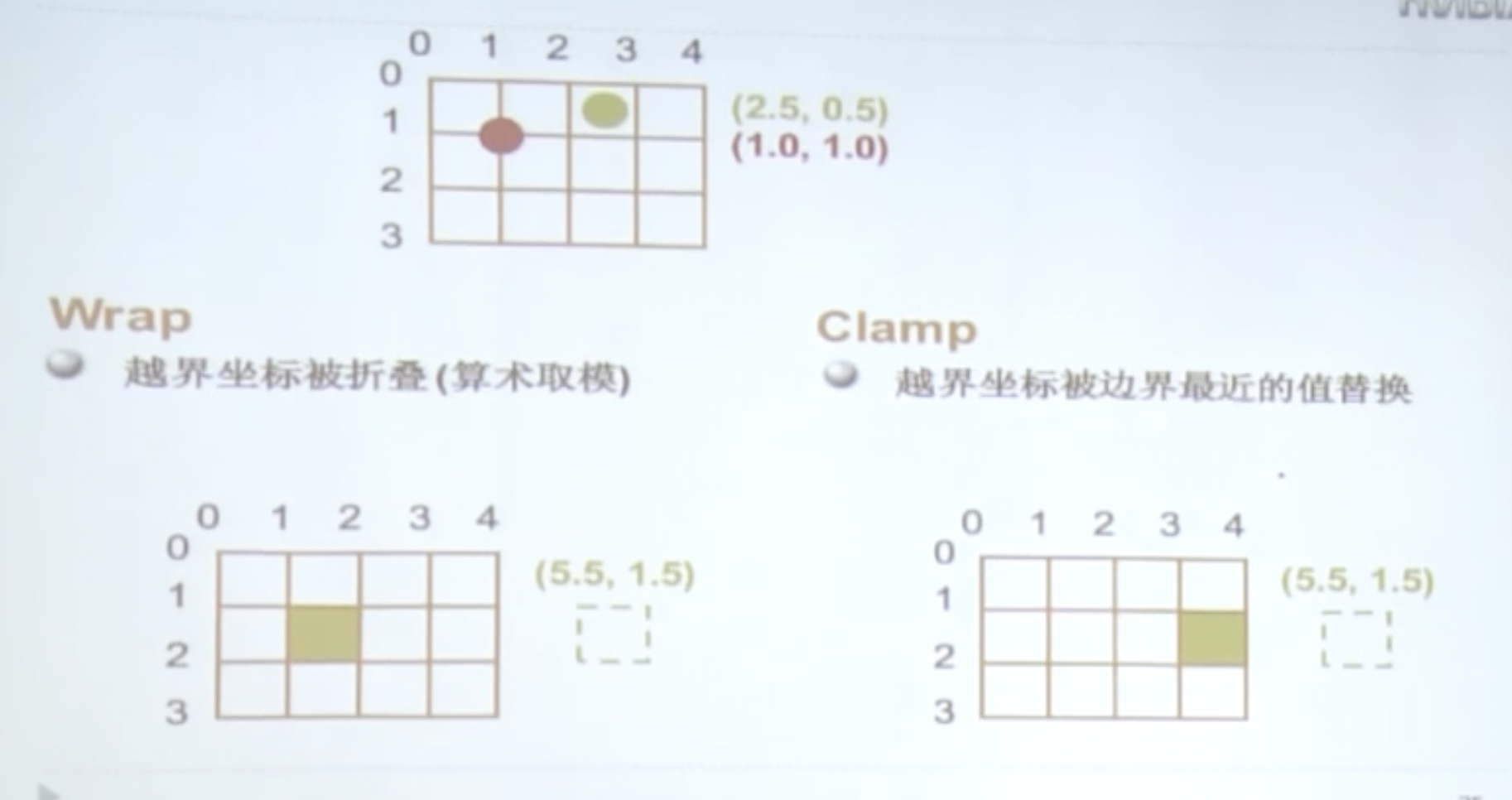
Texture代码请查看《CUDA c program》

GPU硬件在数据的并行计算问题上，怎样可以达到很好的性能？

• 有效利用并行性
• 尽可能合并内存访问
• 利用shared memory
• 开发其他可存储空间（Texture、Constant）
• 减少bank冲突

SM资源动态分割

SM资源分配使用木桶原理。谁的资源先达到瓶颈则减少该部分资源的分配。

例子：

假设我们有768个线程（3个block），每个线程用10个寄存器。然而寄存器的大小最多只支持10个寄存器，如果此时每个线程分配11个寄存器，那么可使用的寄存器数量不够，则会自动减少block数量，变为512个线程（2个block），每个线程使用的11个寄存器，剩余的线程就会变为空闲状态。

数据预读

在一次global memory读操作和实际用到这个数据的语句中间，插入独立于以上数据的指令，可以隐藏访问延迟(并行)。

1
2
3

float m = Md[i]; //Read global memory
float f = a * b  + c * d; //执行指令，不依赖读内存的操作。该语句可以被隐藏延迟。
float f2 = m * f;

引入预读操作的瓦片化matrix multiply

1
2
3
4
5
6
7
8
9

// Load first tile into registers
for (/*...*/)
{
  	// 将寄存器的内容读取到shared memory
  	__syncthreads();
  	// Load下一个tile到寄存器
  	// 执行乘累加操作
  	__syncthreads();
}

指令混合

计算密集型任务很容易受限于带宽，典型的情况就是在存储器和执行配置优化完成后，考虑指令优化。

比如：

除以2^n，采用>>n

以2^n求模，采用&(2^n - 1)

避免double到float的类型自动转换

循环展开

example:

1
2
3
4

for (int k = 0; k < BLOCK_SIZE; ++k) 
{
  	Pvalue += Ms[ty][k] * Ns[k][tx];
}

虽然这条语句只是单纯的循环计算，但是系统需要做很多额外的操作。

改成：

1
2
3
4

Pvalue += Ms[ty][0] * Ns[0][tx] + 
  				Ms[ty][1] * Ns[1][tx] + 
  				...
  				Ms[ty][15] * Ns[15][tx]; // BLOCK_SIZE = 16

去掉循环的好处：不再有循环计数器更新，不再有分支，常量索引（不再有地址运算）。

编译自动实现：

1
2
3
4
5

#pragma unroll BLOCK_SIZE
for (int k = 0; k < BLOCK_SIZE; ++k) 
{
  	Pvalue += Ms[ty][k] * Ns[k][tx];
}

缺点：可扩展性不强

最后修改于 2023-08-08