深度学习(6-7节)
优化算法
Mini-batch梯度下降法
假设我们的样本数量为500w个,那么在进行梯度下降之前,我们需要先将500w个数据整合成一个大的向量$X$。Mini-batch的做法为将500w个样本按照每个子集为1000个样本等分。每个子集标记为$X^{\left{ 1\right} }X^{\left{ 2\right} },\dots,X^{\left{ 5000\right} }$。相应的,除了需要拆分$X$,也需要拆分标签$Y$,拆分的方法和$X$相同。
Mini-batch的原理是将同时原本对所有样本和标签同时进行梯度下降转变为同时只对一个子集进行梯度下降处理,处理5000次。需要注意代价函数也要改变,因为每次训练的样本个数改变了。
当你的训练集大小很大的时候,mini-batch梯度下降法比batch梯度下降法运行地更快。
batch梯度下降法和Mini-batch梯度下降法的代价随迭代的图像如下:
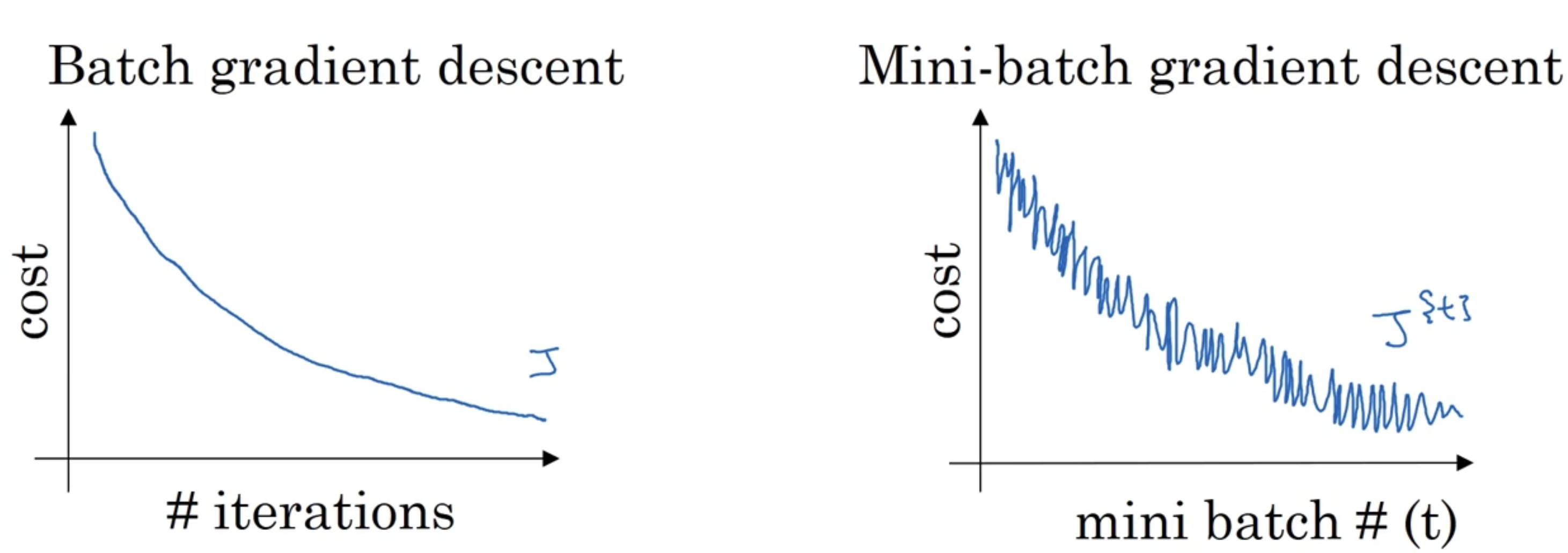
右边的图像出现波动的原因是:每次实现梯度下降的样本集不同,可能$X^{\left{ 1\right} }$和$Y^{\left{ 1\right} }$需要花费的代价更大,而$X^{\left{ 2\right} }$和$Y^{\left{ 2\right} }$花费的代价更少,从而形成一个噪声的现象。
那么mini-bash的大小如何决定呢?
先看两种极端情况:
如果子集的大小为m,那么mini-bash梯度下降就变成了batch梯度下降;
如果子集的大小为1,那么mini-bash梯度下降就变成了随机梯度下降法,每个样本都是一个子集;
batch梯度下降每次下降的噪声会小一点,幅度会大一点(这里的噪声是指梯度下降的方向偏离目标);而随机梯度下降大部分时间会向着全局最小值逼近,但有时候会远离最小值(刚好该样本是一个’‘坏’‘样本),随机梯度下降法永远不会收敛,而是会一直在最小值附近波动。
batch梯度下降在训练数据很大的时候,单次训练迭代时间过长,如果训练数据量较小的情况下效果较好;而随机梯度下降单次迭代很快,但却无法使用向量化技术对运算进行加速。我们的目的就是选择一个不大不小的size,使得我们的学习速率达到最快(梯度下降)。
最优的情况就是,单次选取的size大小的数据分布比较符合整体数据的分布,这样使得学习速率和运行效率都比较高。
指数加权平均
指数加权平均也称指数加权移动平均,通过它可以来计算局部的平均值,来描述数值的变化趋势,下面通过一个温度的例子来详细介绍一下。
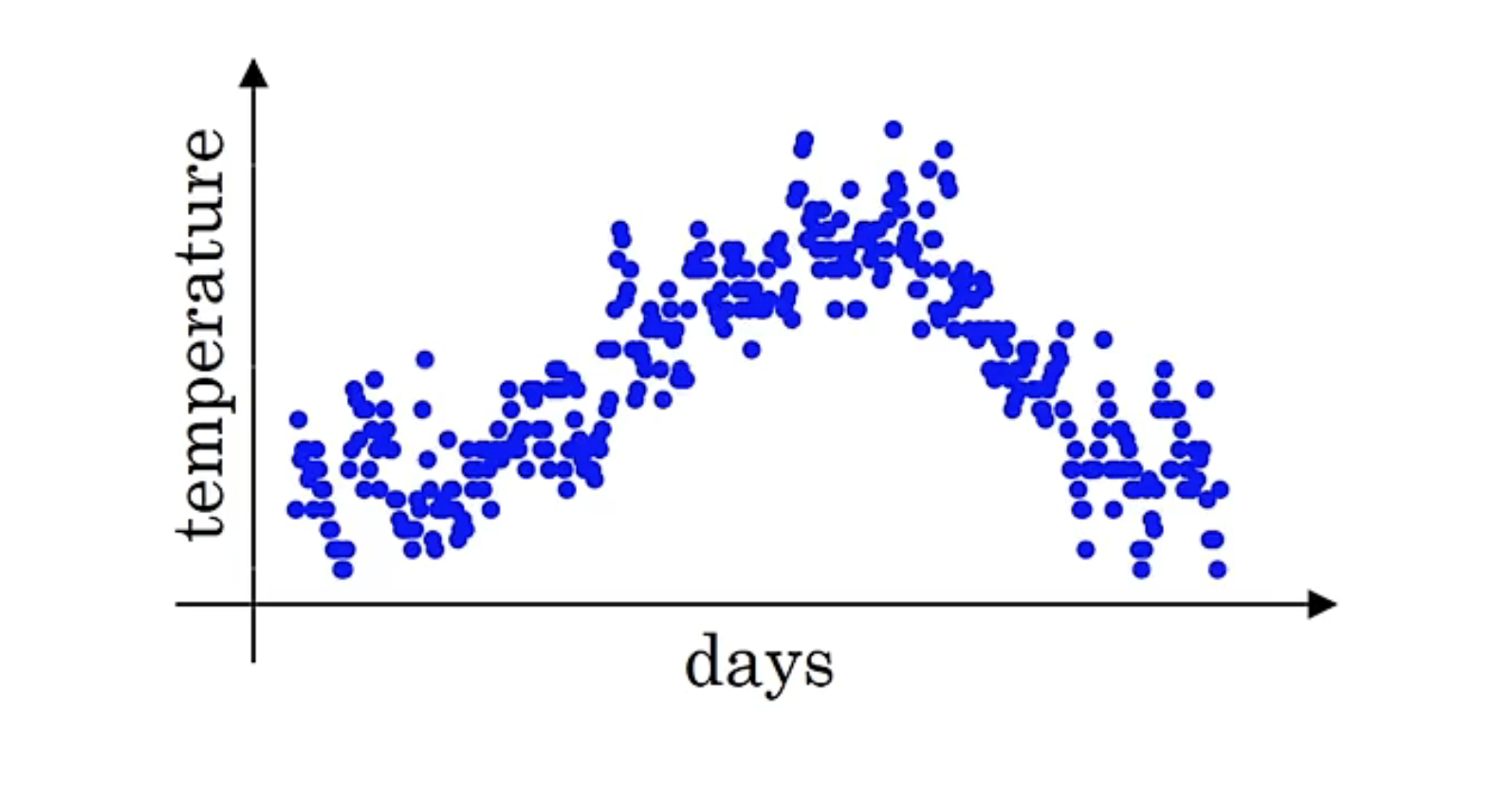
上图是温度随时间变化的图像,我们通过温度的局部平均值(移动平均值)来描述温度的变化趋势,计算公式如下:
$$
v_t=\beta v_{t-1}+(1-\beta)\theta_{t}\
v_0=0\
v_1=0.9v_0+0.1\theta_1\
v_2=0.9v_1+0.1\theta_2\
\theta 代表当天的温度,v代表局部平均值
$$
当$\beta$为0.9时,可以将$v_t$看作$\frac{1}{1-\beta}=\frac{1}{1-0.9}=10$天的平均值。
当$\beta$变得越小,移动平均值的波动越大。
通过上面的公式往下推到,可以得到$v_{100}$的表达式:
$$
v_{100}=0.1\times\theta_{100}+0.1\times0.9\times\theta_{99}+\dots+0.1\times0.9^{99}\times\theta_1\
=0.1\times\sum_{i=1}^{100}0.9^{100-i}\times\theta_i
$$
当$\epsilon=1-\beta$时,$(1-\beta)^{\frac{1}{\epsilon}}\approx\frac{1}{e}\approx\frac{1}{1-\beta}$,所以可以将$v_t$看作$\frac{1}{1-\beta}=\frac{1}{1-0.9}=10$天的平均值。
简单来说,普通的加权求平均值的方法每一项的权重是$\frac{1}{n}$,指数加权平均每一项的权重是指数递减的。
由于我们初始设置的$v_0$为0,这样会使前面几个$v_1,v_2\dots$的值与实际值相比偏小,我们通常会采取以下的办法来修正偏差:
$$
v_t=\frac{\beta v_{t-1}+(1-\beta)\theta_t}{1-\beta^t}
$$
这样修正的效果为随着t的增加,分母越来越接近1。相当于时间越短,修正的幅度越大,所以这个公式主要是为了修正早期的偏差。
动量梯度下降法
我们将上面所说的指数加权平均的做法应用于神经网络的反向传播过程,如下:
$$
V_{dW}=\beta V_{dW}+(1-\beta)dW\
V_{db}=\beta V_{db}+(1-\beta)db\
W:=W-\alpha V_{dW},b:=b-\alpha V_{db}
$$
这样做可以减缓梯度下降的幅度,因为梯度下降不一定朝着最快的方向前进。如下图所示:

原本为蓝色的梯度下降会变成红色,纵轴摆动的方向变小了且上下摆动的幅度均值大概为0。这样一来,即使我增加学习率或者步长也不会出现紫色线这种偏离函数的情况。
$\beta$最常用的值为0.9,按照道理来说需要加上偏差修正。但实际上不会这么做,因为经过10次迭代之后,移动平均已经过了初始阶段,不再是一个具有偏差的预测值。
RMSprop算法
通过前面的算法可知,我们加快学习效率的方法是增加$W$方向的学习速率(图中的水平方向),降低$b$方向的学习速率(垂直方向)。公式如下:
$$
S_{dW}=\beta S_{dW}+(1-\beta)(dW)^2\
S_{db}=\beta S_{db}+(1-\beta)(db)^2\
W:=W-\alpha\frac{dW}{\sqrt{S_{dW}}+\epsilon}\
b:=b-\alpha\frac{db}{\sqrt{S_{db}}+\epsilon}\
式中,S_{dW}和S_{db}表示权重W和偏置值b在t−1轮迭代中的梯度动量\
超参数β一般取值为0.9,学习率\alpha一般取值为 0.001,ε是防止分母为零,一般去10^{-8}。
$$
我们会希望$S_{db}$较大,$S_{dW}$较小,这样可以使得$W$方向的变化更大,$b$方向的变化更小。结果变化如下图:

Adam算法
Adam算法是将动量梯度下降法和RMSprop算法结合起来,公式如下:
$$
首先初始化V_{dW}=0,S_{dW}=0,V_{db}=0,S_{db}=0\
在第t次迭代时:\
使用当前的mini-batch计算dW,db\
V_{dW}=\beta_1V_{dW}+(1-\beta_1)dW,V_{db}=\beta_1V_{db}+(1-\beta)db\quad 动量梯度下降\
S_{dW}=\beta_2S_{dW}+(1-\beta_2)(dW)^2,S_{db}=\beta_2S_{db}+(1-\beta_2)(db)^2\quad SMSprob\
V_{dW}^{correct}=\frac{V_{dW}}{1-(\beta_1)^t},V_{db}^{correct}=\frac{V_{db}}{1-(\beta_1)^t}\
S_{dW}^{correct}=\frac{S_{dW}}{1-(\beta_2)^t},S_{db}^{correct}=\frac{S_{db}}{1-(\beta_2)^t}\
W:=W-\alpha\frac{V_{dW}^{correct}}{\sqrt{S_{dW}^{corret}}+\epsilon}\
b:=b-\alpha\frac{V_{db}^{correct}}{\sqrt{S_{db}^{corret}}+\epsilon}\
$$
Adam算法被证明具有更强的普适性,适用于更加广泛的结构。
其中上述算法中的超参数使用值:
$$
\alpha是一个需要不断调整的值\
\beta_1推荐值为0.9\
\beta_2推荐值为0.999\
\epsilon推荐值为10^{-8}
$$
学习率衰减
假设使用一个mini-batch的梯度下降方法,梯度下降会出现噪声,最后不会收敛,而是会在最小值之间波动。通过学习率衰减的办法,可以使得在梯度下降到最小值附近,波动的幅度变得很小。如下图所示(从蓝线到绿线的变化):

学习率的设置公式如下:
$$
\alpha=\frac{1}{1+衰减率\times 代数}\alpha_0\
这里的代数是指迭代的次数,衰减率和\alpha是一个需要调整的参数。
$$
作业五
分别使用mini-batch,动量梯度下降,Adam算法对梯度下降进行加速。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
|
# 导入库
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 参数更新
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
Update parameters using one step of gradient descent
Arguments:
parameters -- python dictionary containing your parameters to be updated:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients to update each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate -- the learning rate, scalar.
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Update rule for each parameter
for i in range(L):
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(i + 1)] -= learning_rate * grads["dW" + str(i + 1)]
parameters["b" + str(i + 1)] -= learning_rate * grads["db" + str(i + 1)]
### END CODE HERE ###
return parameters
# mini-batch
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
np.random.seed(seed) # To make your "random" minibatches the same as ours
m = X.shape[1] # number of training examples
mini_batches = []
# Step 1: Shuffle (X, Y) 洗牌
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, k * mini_batch_size : (k + 1) * mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k + 1) * mini_batch_size]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# Handling the end case (last mini-batch < mini_batch_size) 处理最后一个mini-batch小于64的情况。
if m % mini_batch_size != 0:
### START CODE HERE ### (approx. 2 lines)
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
### END CODE HERE ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
# 动量梯度下降:1.初始化参数 2.更新参数
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
Returns:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
# Initialize velocity
for i in range(L):
### START CODE HERE ### (approx. 2 lines)
v['dW' + str(i + 1)] = np.zeros(parameters["W" + str(i + 1)].shape)
v['db' + str(i + 1)] = np.zeros(parameters["b" + str(i + 1)].shape)
### END CODE HERE ###
return v
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Momentum update for each parameter
for i in range(L):
### START CODE HERE ### (approx. 4 lines)
# compute velocities
v['dW' + str(i + 1)] = beta * v['dW' + str(i + 1)] + (1 - beta) * grads['dW' + str(i + 1)]
v['db' + str(i + 1)] = beta * v['db' + str(i + 1)] + (1 - beta) * grads['db' + str(i + 1)]
# update parameters
parameters['W' + str(i + 1)] -= learning_rate * v['dW' + str(i + 1)]
parameters['b' + str(i + 1)] -= learning_rate * v['db' + str(i + 1)]
### END CODE HERE ###
return parameters, v
# Adma算法: 1.初始化V[dW],V[db],S[dW],S[db] 2.更新参数
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s".
for i in range(L):
### START CODE HERE ### (approx. 4 lines)
v["dW" + str(i + 1)] = np.zeros(parameters["W" + str(i + 1)].shape)
v["db" + str(i + 1)] = np.zeros(parameters["b" + str(i + 1)].shape)
s["dW" + str(i + 1)] = np.zeros(parameters["W" + str(i + 1)].shape)
s["db" + str(i + 1)] = np.zeros(parameters["b" + str(i + 1)].shape)
### END CODE HERE ###
return v, s
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2 # number of layers in the neural networks
v_corrected = {} # Initializing first moment estimate, python dictionary
s_corrected = {} # Initializing second moment estimate, python dictionary
# Perform Adam update on all parameters
for i in range(L):
# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
### START CODE HERE ### (approx. 2 lines)
v["dW" + str(i + 1)] = beta1 * v["dW" + str(i + 1)] + (1 - beta1) * grads["dW" + str(i + 1)]
v["db" + str(i + 1)] = beta1 * v["db" + str(i + 1)] + (1 - beta1) * grads["db" + str(i + 1)]
### END CODE HERE ###
# Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
### START CODE HERE ### (approx. 2 lines)
v_corrected["dW" + str(i + 1)] = v["dW" + str(i + 1)] / (1 - beta1 ** t)
v_corrected["db" + str(i + 1)] = v["db" + str(i + 1)] / (1 - beta1 ** t)
### END CODE HERE ###
# Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
### START CODE HERE ### (approx. 2 lines)
s["dW" + str(i + 1)] = beta2 * s["dW" + str(i + 1)] + (1 - beta2) * np.multiply(grads["dW" + str(i + 1)], grads["dW" + str(i + 1)])
s["db" + str(i + 1)] = beta2 * s["db" + str(i + 1)] + (1 - beta2) * np.multiply(grads["db" + str(i + 1)], grads["db" + str(i + 1)])
### END CODE HERE ###
# Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
### START CODE HERE ### (approx. 2 lines)
s_corrected["dW" + str(i + 1)] = s["dW" + str(i + 1)] / (1 - beta2 ** t)
s_corrected["db" + str(i + 1)] = s["db" + str(i + 1)] / (1 - beta2 ** t)
### END CODE HERE ###
# Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
### START CODE HERE ### (approx. 2 lines)
parameters["W" + str(i + 1)] -= learning_rate * v_corrected["dW" + str(i + 1)] / (epsilon + np.sqrt(s_corrected["dW" + str(i + 1)]))
parameters["b" + str(i + 1)] -= learning_rate * v_corrected["db" + str(i + 1)] / (epsilon + np.sqrt(s_corrected["db" + str(i + 1)]))
### END CODE HERE ###
return parameters, v, s
|
使用不同算法加速的模型进行预测:
1
2
|
# 加载数据
train_X, train_Y = load_dataset()
|
数据分布如下:
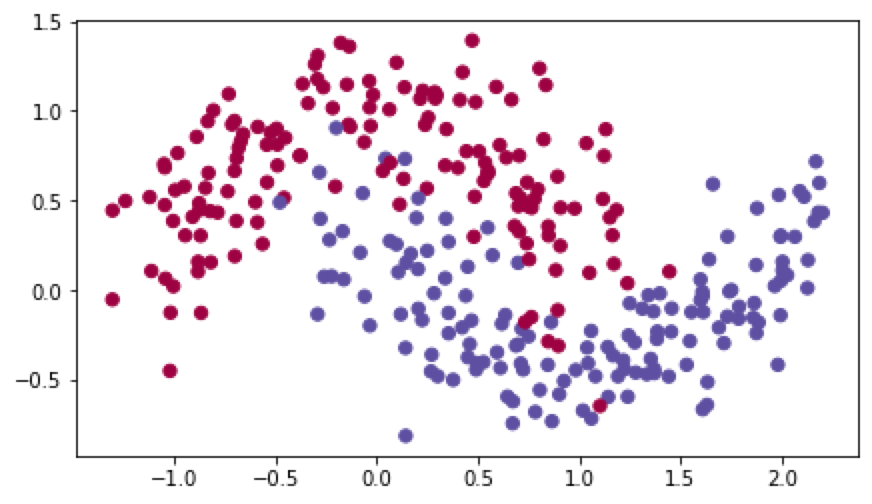
建立预测模型并使用三种不同的算法进行加速预测模型:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
|
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
"""
3-layer neural network model which can be run in different optimizer modes.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
layers_dims -- python list, containing the size of each layer
learning_rate -- the learning rate, scalar.
mini_batch_size -- the size of a mini batch
beta -- Momentum hyperparameter
beta1 -- Exponential decay hyperparameter for the past gradients estimates
beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
num_epochs -- number of epochs
print_cost -- True to print the cost every 1000 epochs
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(layers_dims) # number of layers in the neural networks
costs = [] # to keep track of the cost
t = 0 # initializing the counter required for Adam update
seed = 10 # For grading purposes, so that your "random" minibatches are the same as ours
# Initialize parameters
parameters = initialize_parameters(layers_dims)
# Initialize the optimizer
if optimizer == "gd":
pass # no initialization required for gradient descent
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# Optimization loop
for i in range(num_epochs):
# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
seed = seed + 1
minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Forward propagation
a3, caches = forward_propagation(minibatch_X, parameters)
# Compute cost
cost = compute_cost(a3, minibatch_Y)
# Backward propagation
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# Update parameters
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam counter
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
# Print the cost every 1000 epoch
if print_cost and i % 1000 == 0:
print ("Cost after epoch %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters
# 画图
def plot_decision_boundary(model, X, y):
#import pdb;pdb.set_trace()
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
y = y.reshape(X[0,:].shape)#must reshape,otherwise confliction with dimensions
plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
plt.show()
|
mini-batch:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
#--------------------------------------------- mini-batch
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
|
cost随迭代次数的变化结果如下:
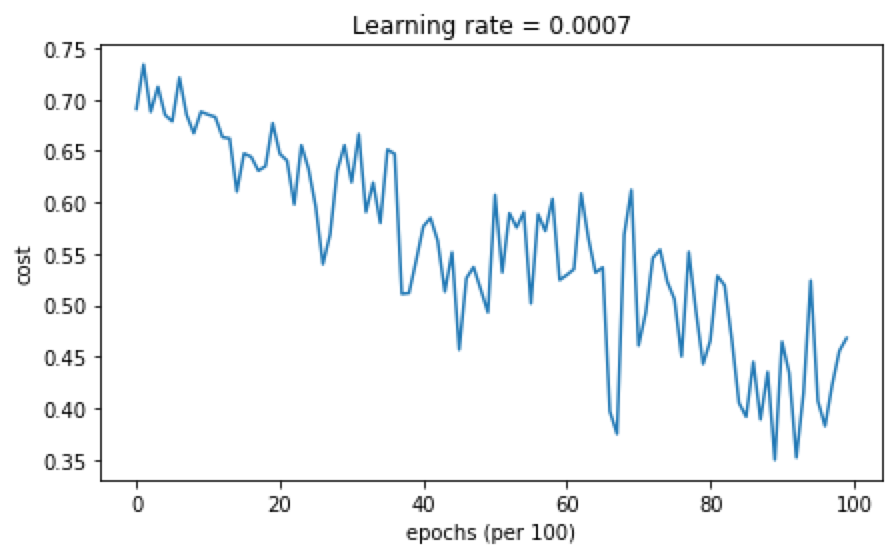
准确率为0.79,分类结果分布如下:

动量下降(with mini-batch):
1
2
3
4
5
6
7
8
9
10
11
12
13
|
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
|
cost随迭代次数的变化结果如下:
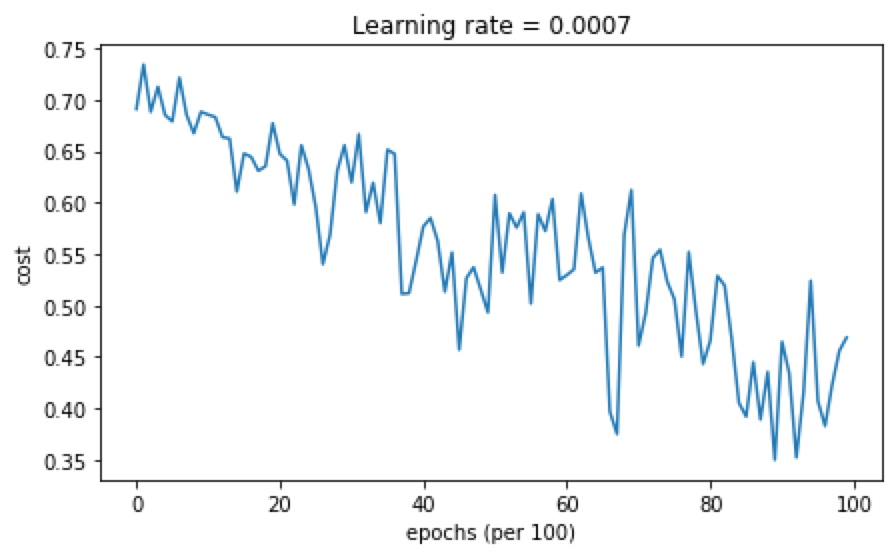
准确率为0.79,分类结果分布如下:
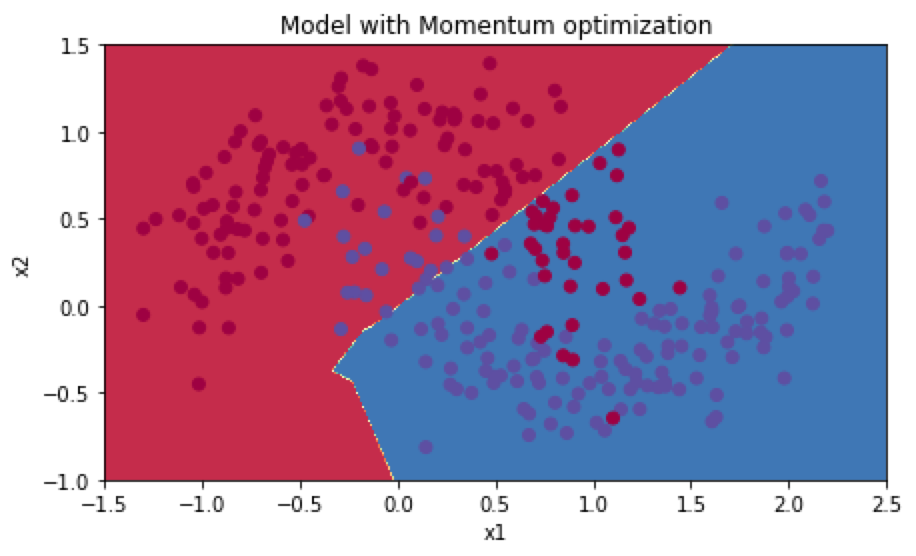
Adma算法(with mini-batch):
1
2
3
4
5
6
7
8
9
10
11
12
13
|
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
|
cost随迭代次数的变化结果如下:
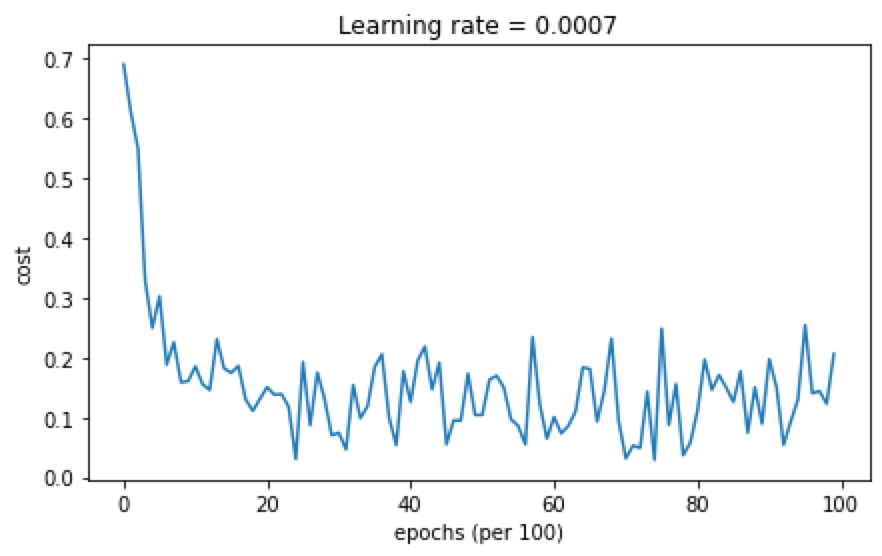
准确率为0.94,分类结果分布如下:

超参数调试
调试处理
超参数一般有:学习率$\alpha$;动量梯度下降的$\beta$;Adma算法的$\beta_1,\beta_2,\epsilon$;神经网络的层数layers;隐藏层的数量;学习率衰减;mini-bash size等。
我们一般优先选择调试学习率$\alpha$,其次是隐藏层数量,mini-batch size和动量下降中的$\beta$。再其次调整的参数就是layers和学习率衰减了。Adma算法的三个参数一般设置为$\beta1=0.9,\beta_2 = 0.999,\epsilon=10^{-8}$,我们一般不会调整它。
在深度学习中,我们一般会通过矩阵随机取值的方式来调参,如下图:
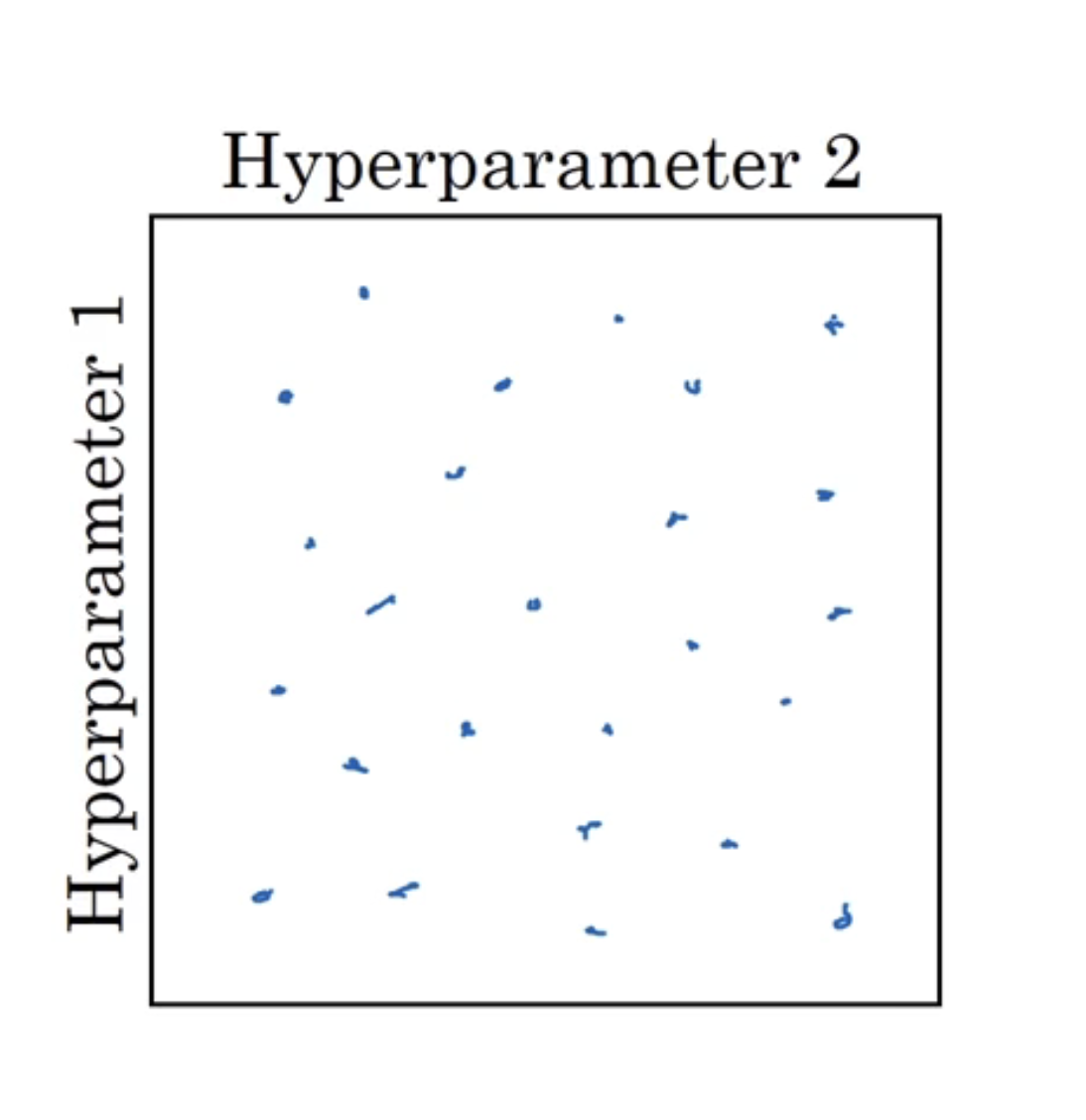
长宽分别代表超参数1,2的取值。一般会在矩阵内随机取25个点来查看效果,因为这样会得到25个不同的超参数1和25个不同的超参数2。
但如果为3个参数,那么我们可以在一个立方体内随机选择点。
超参数调试的技巧是从粗糙到精细的过程:经过粗略的调整,发现在某区域内效果较好,那么我们要做的是,放大这块区域,更加密集的取值,来获取最优点。
为超参数选择合适的范围
上面所说的随机取值并不是在有效值范围内的随机均匀取值,而是选择合适的步进值来探究超参数。对于隐藏层和隐藏单元的数量,随机均匀取值是合理的,但对某些参数的不合理的。
假设你认为学习率$\alpha$的取值范围是0.0001~1,取值范围内随机均匀取值会将90%的值集中在0.1到1里面,不合理。对于这种情况,一般先按0.0001,0.001,0.01,0.1,1作为分界点,在分界点之间随机均匀取值。
在Python中你可以这样做:
1
2
3
4
5
6
|
import numpy as np
r = -4 * np.random.rand()
a = np.power(10, r)
# 更多的取值情况为10^a~10^b
# 通过计算得到a和b的值,然后我们将r取值变为a~b之间的随机取值。
|
还有就是动量梯度下降$\beta$的取值,它意味着指数加权平均的大小,一般通过$1-\beta$来取范围。但因为是$1-\beta$,需要将排列顺序颠倒。
1
2
3
4
5
6
7
|
import numpy as np
# r在[-3, -1]内
h = -1
l = -3
r = (h - l) * np.random.rand() + l
beta = 1 - np.power(10, r)
|
超参数训练方式:Panda VS Caviar
如果没有很大的算力的情况下,可以根据天数来调整超参数来观察效果(每次只能运行一个模型)。(Panda)
在算力足够的情况下,同时训练不同的几个模型。(Caviar)
归一化网络
前面介绍过的输入归一化,可以使梯度下降时,更加不容易偏离方向,增大步长,加快学习速度。但这只针对了输入层,如果我们对所有隐藏层进行归一化,可以大大加快学习速率,这就是我们平常所说的batch归一化。实际做法一般是对$Z^{[l]}$进行归一化处理,做法如下:
$$
对于某一层的Z^{[l]},有z^{(1)},z^{(2)},\dots,z^{(m)}\
u=\frac1m\sum_{i=1}^mz^{(i)}\
\sigma^2=\frac1m\sum_{i=1}^m(z^{(i)}-u)^2\
z_{norm}^{(i)}=\frac{z^{(i)}-u}{\sqrt{\sigma^2+\epsilon}}\
这样Z的每一个分量z值都已经标准化了,平均值为0,方差为1;\
但我们不想让隐藏单元总是含有平均值0和方差1,也许隐藏单元有不同的分布会有意义。\
\tilde{z}^{(i)}=\gamma z^{(i)}{norm}+\beta\
这里的\gamma和\beta的作用是让你可以构造其他平均值和方差的隐藏单元值\
如果\gamma=\sqrt{\sigma^2+\epsilon},\beta=u\quad则\tilde{z}^{(i)}=z^{(i)}{normal}
$$
已经知道了如何对Z进行归一化,那么如何将其应用于神经网络中呢?
BatchNormal神经网络参数计算的过程如下:
$$
X \xrightarrow{W^{[1]},b^{[1]}}Z^{[1]} \xrightarrow[Batch Normal(BN)]{\gamma^{[1]},\beta^{[1]}}\tilde{z}^{[i]}\rightarrow a^{[1]}=g^{[1]}(\tilde{z}^{[i]}) \xrightarrow{W^{[2]},b^{[2]}}Z^{[2]}\rightarrow\dots
$$
需要注意的是这里的$\gamma$和$\beta$是和$W$,$b$一样的参数,而不是超参数。所以在反向传播时,也需要计算$d\beta,d\gamma$来更新$\beta$和$\gamma$的值。而且常数项$b$代表变化后的Z平均值离0有多远,但是标准化之后的$z^{(i)}_{norm}$均值必定为0,所以我们可以直接将$b$去掉,转而使用后面的$\beta$参数来定义。
Batch Normal为什么奏效?
用一个例子来解释就是:你的训练集都是黑猫或者其他动物,假设他们都分布于某一侧,将训练出来的模型去预测花色猫,效果就不好。花猫分布于另一侧,这样相当于不同于黑猫的x分布。你不能期待分布在左边的数据训练出来的模型能预测右边的数据。假设将左侧的数据进行Batch Normal,相当于人为将其分布均匀,比较能适应新的数据集,防止了Covarite shift。
放在深层神经网络来看就是前层参数的变化会影响后层的参数,归一化降低了这种影响,尽量只保持特征值带来的波动。
Batch Normal和dropout正则化
dropout正则化对隐藏单元进行随机删除,从而引入噪声,防止对某个神经单元过于依赖。而Batch Normal在每个mini-batch的均值方差与整体的均值方差不一致,引入加性噪声和乘性噪声,导致轻微的正则化。如果想减少这种影响,可以将mini-batch的值设置的更大,从而减少带来的噪声,减少正则化的效果!
测试时的Batch Normal
因为测试时是单个单个进行测试的,不能直接进行batch normal,因为无法知道均值和方差。所以我们使用训练集来估算均值和方差。通常估算的方法是通过指数加权平均来粗略估算均值和方差。
softmax回归
假设我们的分类类别是多个而不是两个,相当于我们的输出层单元个数变成了多个,数量就是你要分出的类别数C。这时,输出层会变成C个概率值,输入为$x$的情况下,输出为$p(类别|x)$,所以输出层是维度为(C,1)的矩阵。
softmax激活函数公式如下:
$$
假设Z^{[L]}=W^{[L]}a^{[L-1]}+b^{[L]},L层有C个隐藏单元,所以Z^{[L]}的维度为(C,1)\
t=e^{(Z^{[L]})}\
a^{[L]}=\frac{t}{\sum_{j=1}^{C}t_j},a_j^{[L]}=\frac{t_i}{\sum_{j=1}^{C}t_j}\
a^{[L]}的维度为(C,1),可以看出softmax激活函数的特点为输入和输出都为(C,1)
$$
使用softmax训练一个softmax分类器
需要注意的是Softmax回归其实就是Logistic回归的推广,当Softmax回归的类C=2,就变成了Logistic回归。
softmax网络的损失函数为:
$$
L(\hat{y},y)=-\sum_{j=1}^Cy_j\log{\hat{y_j}}
$$
代价函数为:
$$
J=\frac1m\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)})
$$
特别需要注意的是,softmax因为是一个多分类的问题,输入的$y$标签也是一个向量,$Y$会变成一个矩阵。比如有猫,狗,牛,蛇,那么蛇的样本标签$y=[0,0,0,1]^{T}$,向量化技术后,整体样本标签会成为一个(C,m)的矩阵。
后向传播的公式:
$$
dz^{[L]}=\hat{y}-y\
$$
深度学习框架
深度学习框架在市面上有很多,我们该如何选择?
作业六
导入需要的库:
1
2
3
4
5
6
7
8
9
10
|
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
from tf_utils import load_dataset, random_mini_batches, convert_to_one_hot, predict
%matplotlib inline
np.random.seed(1)
|
计算损失函数的例子:
1
2
3
4
5
6
7
8
9
10
|
y_hat = tf.constant(36, name='y_hat') # Define y_hat 常量. Set to 36.
y = tf.constant(39, name='y') # Define y. Set to 39
loss = tf.Variable((y - y_hat)**2, name='loss') # Create a variable for the loss
init = tf.global_variables_initializer() # When init is run later (session.run(init)),
# the loss variable will be initialized and ready to be computed
with tf.Session() as session: # Create a session and print the output
session.run(init) # Initializes the variables
print(session.run(loss)) # Prints the loss
|
会话机制:
1
2
3
4
5
6
7
|
a = tf.constant(2)
b = tf.constant(10)
c = tf.multiply(a,b)
print(c)
sess = tf.Session()
print(sess.run(c))
|
往函数喂数据:
1
2
3
4
5
|
# Change the value of x in the feed_dict
x = tf.placeholder(tf.int64, name = 'x')
print(sess.run(2 * x, feed_dict = {x: 3}))
sess.close()
|
初始化神经网络模型参数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
# GRADED FUNCTION: linear_function
def linear_function():
"""
Implements a linear function:
Initializes W to be a random tensor of shape (4,3)
Initializes X to be a random tensor of shape (3,1)
Initializes b to be a random tensor of shape (4,1)
Returns:
result -- runs the session for Y = WX + b
"""
np.random.seed(1)
### START CODE HERE ### (4 lines of code)
X = tf.constant(np.random.randn(3, 1), name="X")
W = tf.constant(np.random.randn(4, 3), name="W")
b = tf.constant(np.random.randn(4, 1), name="b")
Y = tf.add(tf.matmul(W, X), b)
### END CODE HERE ###
# Create the session using tf.Session() and run it with sess.run(...) on the variable you want to calculate
### START CODE HERE ###
sess = tf.Session()
result = sess.run(Y)
### END CODE HERE ###
# close the session
sess.close()
return result
|
激活函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Computes the sigmoid of z
Arguments:
z -- input value, scalar or vector
Returns:
results -- the sigmoid of z
"""
### START CODE HERE ### ( approx. 4 lines of code)
# Create a placeholder for x. Name it 'x'.
x = tf.placeholder(tf.float32, name="x")
# compute sigmoid(x)
sigmoid = tf.sigmoid(x)
# Create a session, and run it. Please use the method 2 explained above.
# You should use a feed_dict to pass z's value to x.
with tf.Session() as sess:
# Run session and call the output "result"
result = sess.run(sigmoid, feed_dict={x:z})
### END CODE HERE ###
return result
|
计算代价函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
# GRADED FUNCTION: cost
def cost(logits, labels):
"""
Computes the cost using the sigmoid cross entropy
Arguments:
logits -- vector containing z, output of the last linear unit (before the final sigmoid activation)
labels -- vector of labels y (1 or 0)
Note: What we've been calling "z" and "y" in this class are respectively called "logits" and "labels"
in the TensorFlow documentation. So logits will feed into z, and labels into y.
Returns:
cost -- runs the session of the cost (formula (2))
"""
### START CODE HERE ###
# Create the placeholders for "logits" (z) and "labels" (y) (approx. 2 lines)
z = tf.placeholder(tf.float32, name="z")
y = tf.placeholder(tf.float32, name="y")
# Use the loss function (approx. 1 line)
cost = tf.nn.sigmoid_cross_entropy_with_logits(logits = z, labels = y)
# Create a session (approx. 1 line). See method 1 above.
sess = tf.Session()
# Run the session (approx. 1 line).
cost = sess.run(cost, feed_dict={z:logits, y:labels})
# Close the session (approx. 1 line). See method 1 above.
sess.close()
### END CODE HERE ###
return cost
|
独热编码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
# GRADED FUNCTION: one_hot_matrix
def one_hot_matrix(labels, C):
"""
Creates a matrix where the i-th row corresponds to the ith class number and the jth column
corresponds to the jth training example. So if example j had a label i. Then entry (i,j)
will be 1.
Arguments:
labels -- vector containing the labels
C -- number of classes, the depth of the one hot dimension
Returns:
one_hot -- one hot matrix
"""
### START CODE HERE ###
# Create a tf.constant equal to C (depth), name it 'C'. (approx. 1 line)
C = tf.constant(value = C, name="C")
# Use tf.one_hot, be careful with the axis (approx. 1 line)
one_hot_matrix = tf.one_hot(labels, C, axis=0)
# Create the session (approx. 1 line)
sess = tf.Session()
# Run the session (approx. 1 line)
one_hot = sess.run(one_hot_matrix)
# Close the session (approx. 1 line). See method 1 above.
sess.close()
### END CODE HERE ###
return one_hot
|
初始化零一向量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
# GRADED FUNCTION: ones
def ones(shape):
"""
Creates an array of ones of dimension shape
Arguments:
shape -- shape of the array you want to create
Returns:
ones -- array containing only ones
"""
### START CODE HERE ###
# Create "ones" tensor using tf.ones(...). (approx. 1 line)
ones = tf.ones(shape)
# Create the session (approx. 1 line)
sess = tf.Session()
# Run the session to compute 'ones' (approx. 1 line)
ones = sess.run(ones)
# Close the session (approx. 1 line). See method 1 above.
sess.close()
### END CODE HERE ###
return ones
|
因为有部分公式可能因为博客插件不支持的原因,完整的笔记请看:
https://github.com/caixiongjiang/deep-learning-computer-vision
最后修改于 2022-07-23

本作品采用
知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。













