深度学习（10-11节）

卷积操作

计算机视觉的例子：

• 图片分类
• 目标检测
• 神经网络实现图片转化迁移

但因为图片的像素高时，每张图片都很是一个很大的维度，如何处理大量的高像素图片呢？这可能就要用到卷积神经网络了。

边缘检测示例

我们通过边缘检测的例子来看卷积操作是如何进行的。

在边缘检测的例子里，卷积核从左到右每列为{1, 1, 1},{0, 0, 0},{-1, -1, -1}。

如图所示，左边是一个6$\times$6的矩阵，中间是一个3$\times$3的卷积核，”*“代表的是卷积操作，但在Python中一般代表乘积的操作，需要注意区分。将卷积核与左边颜色加深的矩阵一一对应相乘后再相加，得到右边绿色的数值。让卷积核在模板上进行移动卷积，可以得到一个4$\times$4的矩阵。假设原图像的维度为m$\times$n，卷积核的大小为a$\times$a，那么得到的矩阵大小为(m-a+1)$\times$(n-a+1)。

对应编程的函数：

python：conv_forward

tensorflow：tf.nn.conv2d

PyTorch：torch.nn.Conv2d

再举个更加明显的例子，如下图：

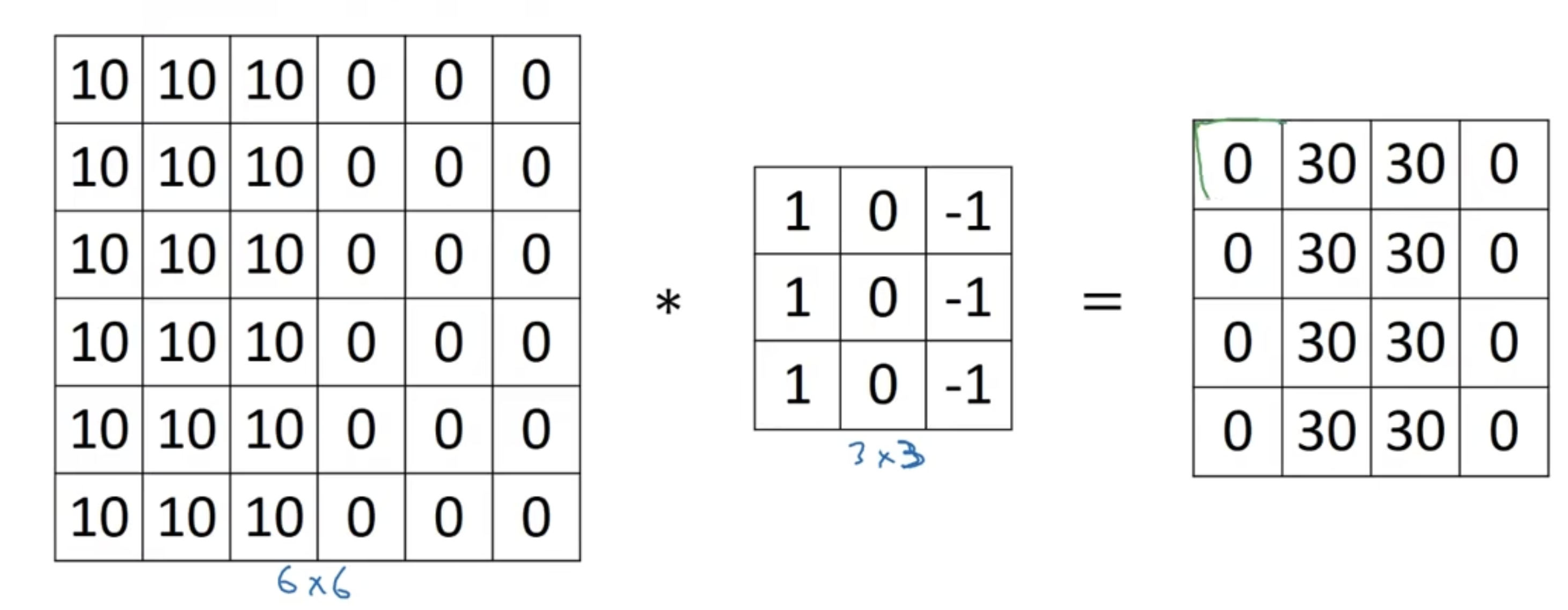
可以看到很明显的就是，如果左边的图片没有变化，与卷积核进行卷积就会得到0，如果选取的区域图片有变化，那么得到的结果就有正值。上述的过程看一看成如下示意图：

将最左边的变化的部分在最右边得到的结果显现出来。

更多的边缘检测内容

在上节例子中的卷积核可以为我们检测由亮到暗的一个过渡的过程，如果是由暗到亮，那么输出的就是负值。

如果我们把上节检测垂直边缘的卷积核旋转一下，从第一行到第三行分别是{1, 1, 1},{0, 0, 0},{-1, -1, -1}，这就变成了一个水平的边缘检测。

列举几个3$\times$3滤波器：

• Sobel滤波器：第一列到第三列分别为：{1, 2, 1},{0, 0, 0},{-1, -2, -1}。
• Scharr滤波器：第一列到第三列分别为：{3, 10, 3},{0, 0, 0},{-3, -10, -3}。

Padding

在进行卷积的过程中，会发现很容易将图像最边缘的部分给忽略掉。一般的做法是在进行卷积之前，会在周围再填充一层像素，这样m$\times$n的矩阵就变成了(m+2)$\times$(n+2)的矩阵，这样在每层神经网络里进行卷积，不会损失掉边缘的特征。

填充一层就代表padding=1，填充两层代表padding=2…

• Valid卷积，其卷积过程如下：

$$ n\times n\quad*\quad f\times f\xrightarrow{no\quad padding}(n-f+1)\times (n-f+1) $$

• Same卷积，顾名思义就是卷积前后的大小是相同的，其卷积过程如下：

$$ n\times n\quad*\quad f\times f\xrightarrow[p=\frac{f-1}{2}]{padding=p}n\times n\ f=2p+1,所以我们的f只取奇数 $$

上述过程中所有填充的像素一般使用0来填充！

卷积步长

卷积步长指得是，卷积模板每次移动的距离，一般用英文stride表示。如果步长表示为$s$，那么卷积后的矩阵大小就变了： $$ n\times n\quad *\quad f\times f\xrightarrow{padding=p,stride=s}\lfloor \frac{n+2p-f}{s}+1 \rfloor \times \lfloor \frac{n+2p-f}{s}+1 \rfloor $$

深度学习的卷积vs数学上的卷积

前面所讲的所有操作都属于深度学习上的卷积，其实这严格意义上来讲不是一种卷积。真正的在数学上的卷积先要对卷积核进行翻转操作，但在深度学习的文献中，我们将直接把深度学习上的伪卷积称为卷积。

三维卷积

我们知道彩色的图像像素矩阵是一个三维矩阵，其中第三个维度为3，代表RGB三个通道。那么如果图像是三维的（假设为6$\times$6$\times$3），那么我们使用的卷积核也应该是三维的（假设为3$\times$3$\times$3），第三个维度与图像的第三个维度是相同的，代表三个通道，但输出图像的结果的形状为4$\times$4$\times$1。

为什么输出的图像是只有一个通道的呢？

可以看一下如下的图来理解：

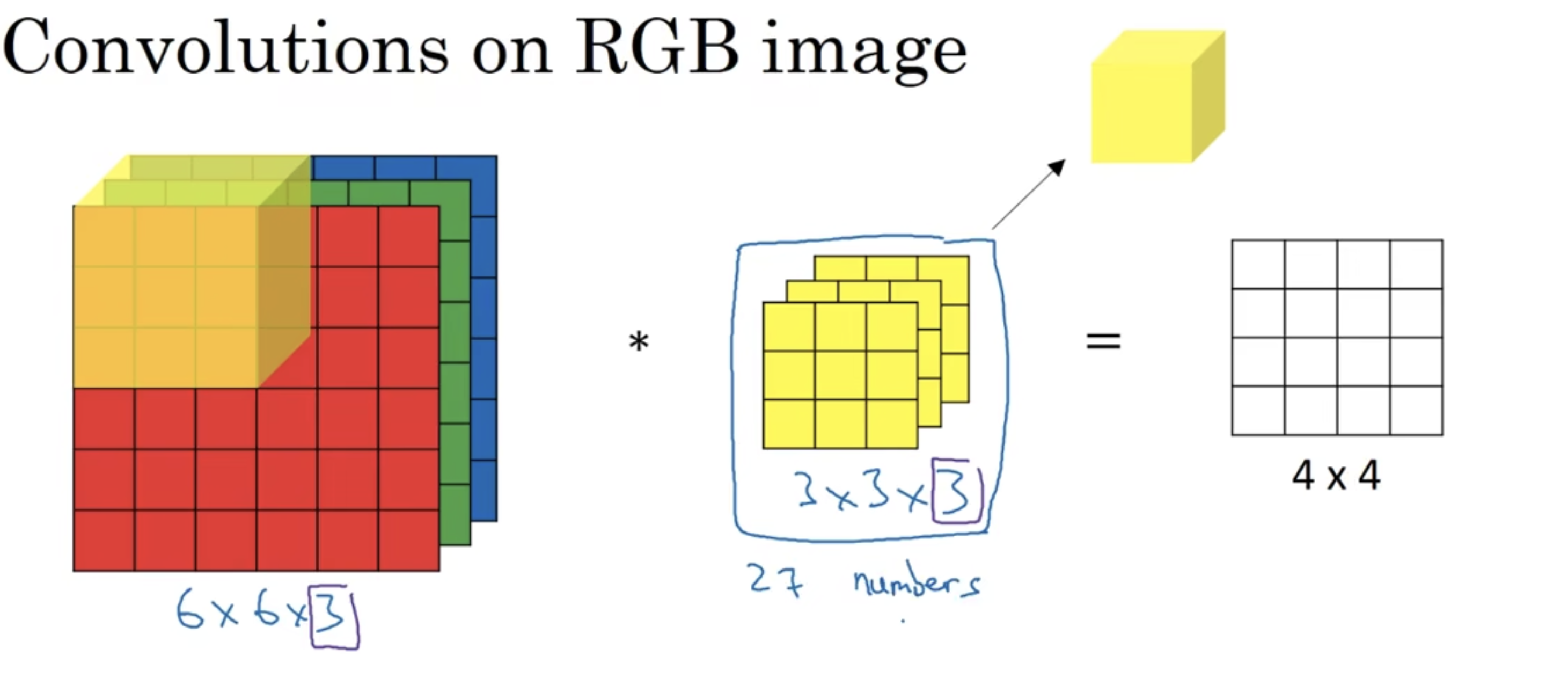
将三个通道的卷积核看成一个长方体，在三通道图像矩阵上进行滑动得到输出。这样做的好处是可以对不同的通道进行不同的卷积模版设置，参数设置不同，可以得到不同的特征检测器。

为了对一个图像同时进行不同特征的选择，我们可以同时用不同的卷积核对图像做卷积，同时得到不同的输出（每个输出都是单通道的），我们将几个输出堆叠在一起，就形成了多维矩阵。注意有几个卷积核，得到图像输出的第三个维度就有几个。

单层卷积网络

学会了三维卷积之后，其实就可以使用三维卷积来表示单层卷积网络的结构了，下面用一个例子来表示过程： $$ input：6\times6\times3\rightarrow\begin{cases} *\quad 3\times3\times3的卷积核 \rightarrow二维图像输出y_1\rightarrow ReLU(y_1+b_1) \ *\quad 3\times3\times3的卷积核 \rightarrow二维图像输出y_2\rightarrow ReLU(y_2+b_2) \end{cases}\ \rightarrow4\times4\times2\quad 这里的2根据单层卷积核的数量进行更改 $$ 和普通的神经网络相比，卷积核相当于普通神经网络中的权重$w$，偏差同样为$b$。一般在使用卷积层时，我们使用$f^{[l]}$来表示第$l$层的卷积核大小；使用$p^{[l]}=padding$代表使用有效填充，也就是same padding，使输入输出前后的图像高度和宽度一致；使用$s^{[l]}$来代表$l$层上的卷积步长；$l$层的输入则变为$n^{[l-1]}_H\times n^{[l-1]}_W\times n^{[l-1]}_c$，$l$层的输出则变为$n^{[l]}_H\times n^{[l]}_W\times n^{[l]}_c$，其中$n^{[l]}_H=\lfloor \frac{n^{[l-1]}_H+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \rfloor$，$n^{[l]}_W=\lfloor \frac{n^{[l-1]}_W+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \rfloor$，第$l$层的卷积核的维度为$f^{[l]}\times f^{[l]}\times n^{[l-1]}_c$，第$l$层的激活值$a^{[l]}$的维度为$n^{[l]}_H\times n^{[l]}_W\times n^{[l]}_c$，如果采用批量梯度下降$m$个样本的激活值$A^{[l]}$的维度为$m\times n^{[l]}_H\times n^{[l]}_W\times n^{[l]}_c$，批量梯度下降的$W$的维度为$f^{[l]}\times f^{[l]}\times n^{[l-1]}_c\times n^{[l]}_c$。

简单卷积网络示例

假设一张$39\times 39$的彩色图像，输入一个三层卷积网络，它的卷积过程如下，所有padding方式都采用no padding，卷积步长初始为1：

• 初始：

$$ n^{[0]}_H=n^{[0]}_W=39,n^{[0]}_c=3\ $$

• 第一层卷积核：

$$ 卷积核大小为f^{[1]}\times f^{[1]}\times n^{[0]}_c,f^{[1]}=3,n^{[0]}_c=3\ 卷积核的数量为n^{[1]}_c=10，卷积步长s^{[1]}=1\ 经过卷积和激活之后a^{[1]}的维度为n^{[1]}_H\times n^{[1]}_W\times n^{[1]}_c，其中n^{[1]}_H=\lfloor \frac{n^{[0]}_H+2p^{[1]}-f^{[1]}}{s^{[1]}}+1 \rfloor=37,同理n^{[1]}_W=37,所以维度为37\times37\times10 $$

• 第二层卷积核：

$$ 卷积核大小为f^{[2]}\times f^{[2]}\times n^{[1]}_c,f^{[2]}=5,n^{[1]}_c=10\ 卷积核的数量为n^{[2]}_c=20,卷积步长s^{[2]}=2\ 经过卷积和激活之后a^{[2]}的维度为n^{[2]}_H\times n^{[2]}_W\times n^{[2]}_c，其中n^{[2]}_H=\lfloor \frac{n^{[1]}_H+2p^{[2]}-f^{[2]}}{s^{[2]}}+1 \rfloor=17,同理n^{[2]}_W=17,所以维度为17\times17\times20 $$

• 第三层卷积核：

$$ 卷积核大小为f^{[3]}\times f^{[3]}\times n^{[2]}_c,f^{[3]}=5,n^{[2]}_c=20\ 卷积核的数量为n^{[3]}_c=40,卷积步长s^{[3]}=2\ 经过卷积和激活之后a^{[3]}的维度为n^{[3]}_H\times n^{[3]}_W\times n^{[3]}_c，其中n^{[3]}_H=\lfloor \frac{n^{[2]}_H+2p^{[3]}-f^{[3]}}{s^{[3]}}+1 \rfloor=7,同理n^{[3]}_W=7,所以维度为7\times7\times40 $$

然后将$a^{[3]}$矩阵中所有的值处理成为一个长向量，并放进logistic层或者softmax层得到预测值。

池化层

• 举一个最大池化层的例子：

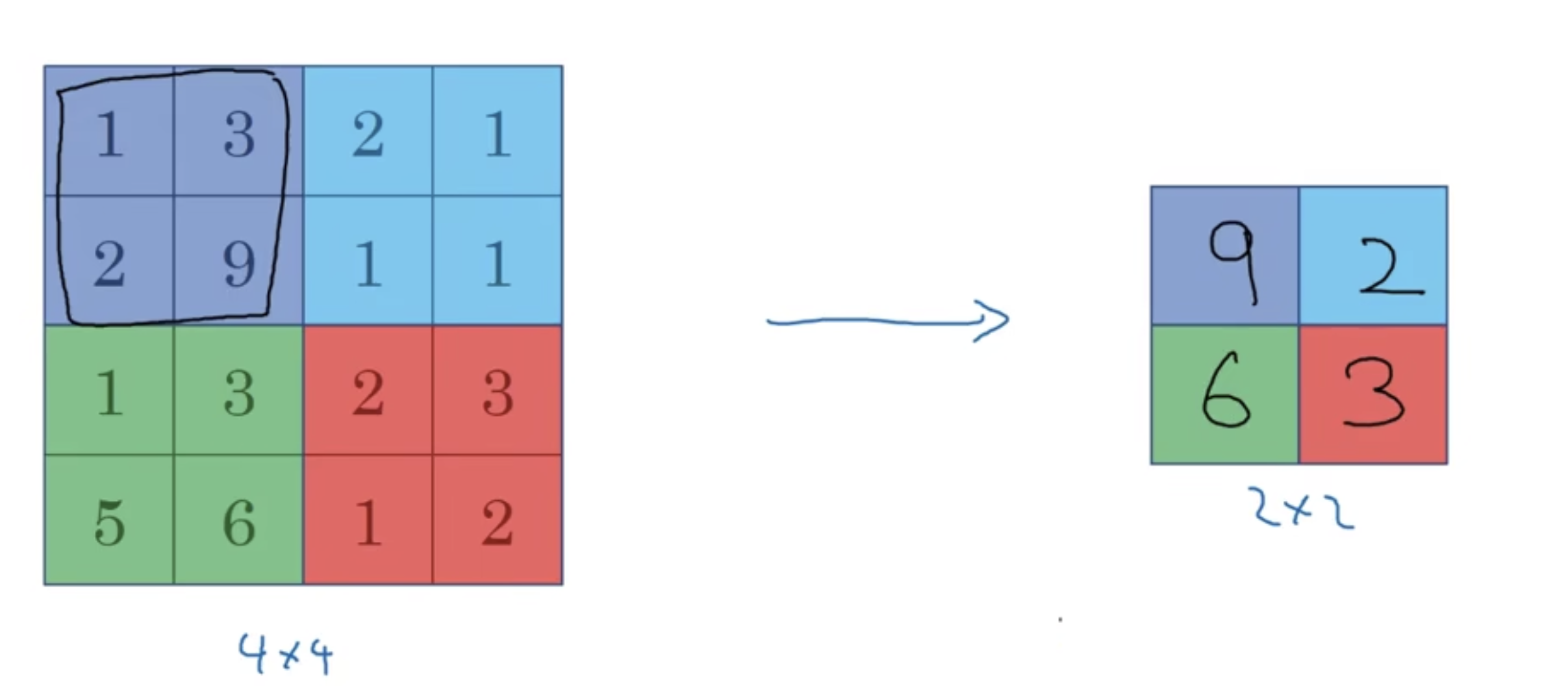
如上一个$4\times 4$的矩阵，将其分成4个部分，在每个部分取最大值，得到一个$2\times 2$的矩阵，这就是一个最大池化的例子。

最大池化只有一组超参数，并没有参数需要进行学习。超参数分别为$f=2,s=2$代表如果类似比作卷积核，卷积核的大小为2，卷积步长为2。如果输入的矩阵是3维的，输出也是3维的，比如输入$5\times5\times2$,输出也是$3\times3\times2$。

• 平均池化：

平均池化的原理和最大池化相同，只是将池化的方式变成了求平均值。

我们在阅读文献时，在计算神经网络使用的层数时，只计算具有参数的层数，只具有超参数的层不参与计算！

对于卷积神经网络的搭建，一般使用别人文章搭建好的超参数来修改，不要自己设置！

一般来说随着卷积神经网络的层数深入，$n_H$和$n_W$会越来越小，$n_c$会原来越大。

常见的卷积神经网络的结构：

conv-pool-conv-pool-FC-FC-FC-softmax

卷积神经网络示例探究

经典网络

• LeNet-5：识别手写数字的经典网络

LeNet-5是针对灰度图片进行训练的。其网络结构如下：

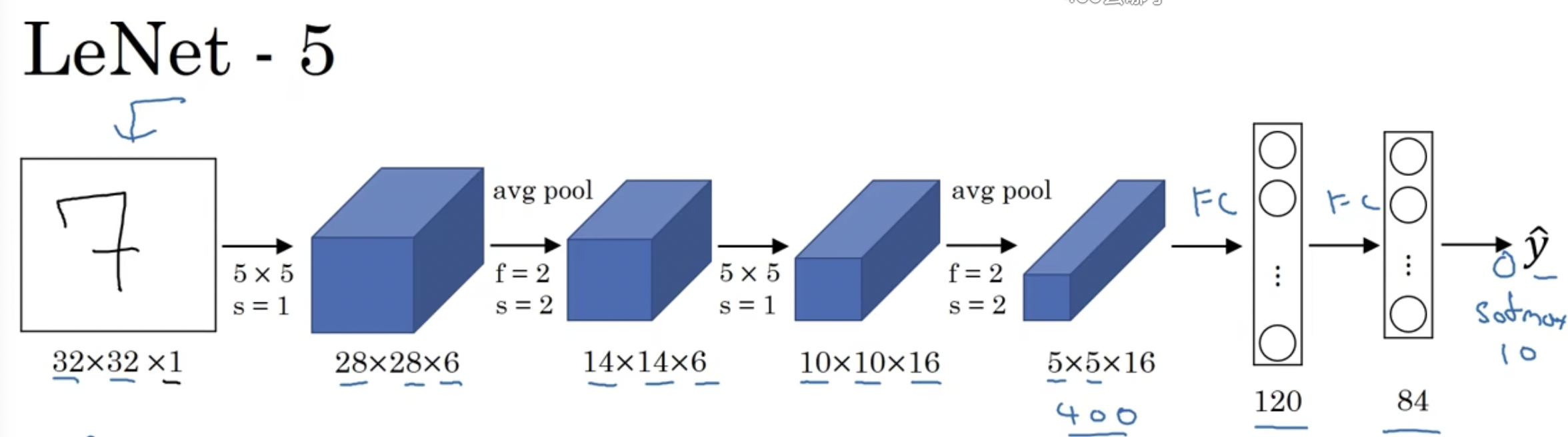
当时早期一般使用平均池化，在现在的版本中，最后输出$\hat{y}$之前会有一个softmax回归层，参数大约为60000个，网络结构较为简单。

• AlexNet

这是针对计算机视觉大赛做的模型，其网络结构如下：

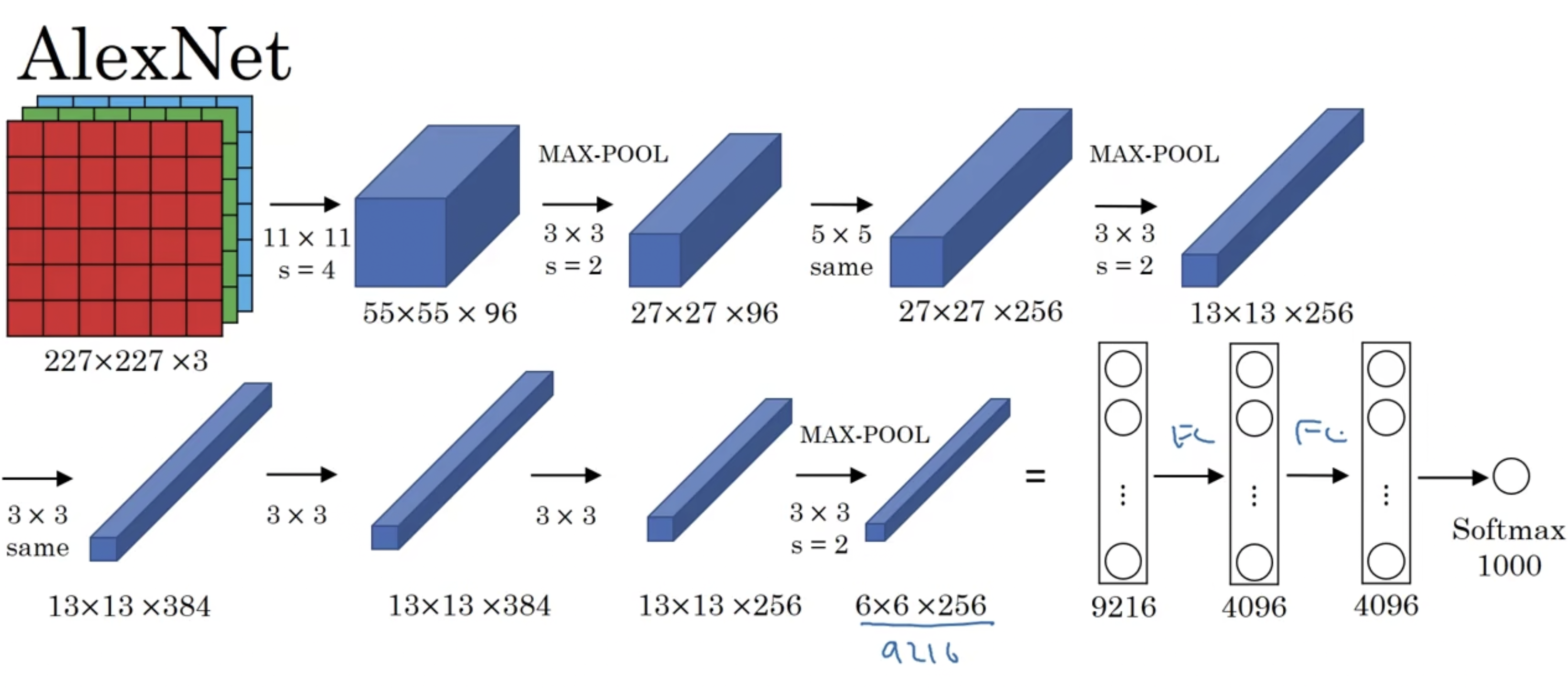
其中图片矩阵的宽和高不变的地方都是因为使用padding填充使得图片的宽高不变。相比LeNet-5网络，该网络的参数大约有6000万个参数。

• VGG-16

网络结构如下：

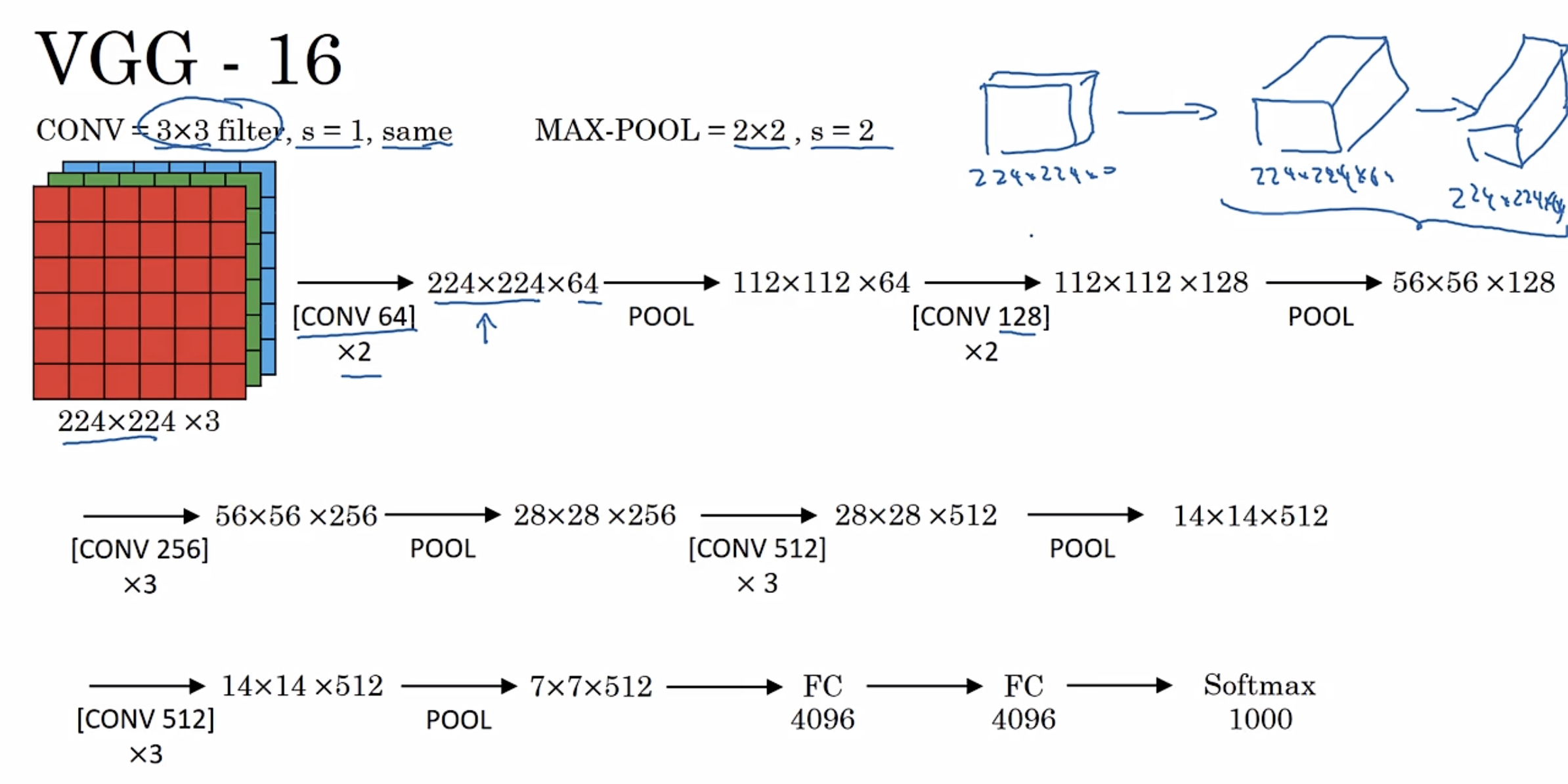
*注意其中的卷积$\times$2代表使用这个卷积层2次。*可以看到它是一个非常深的网络，总共包含大约1.38亿个参数。

残差网络

• 残差块

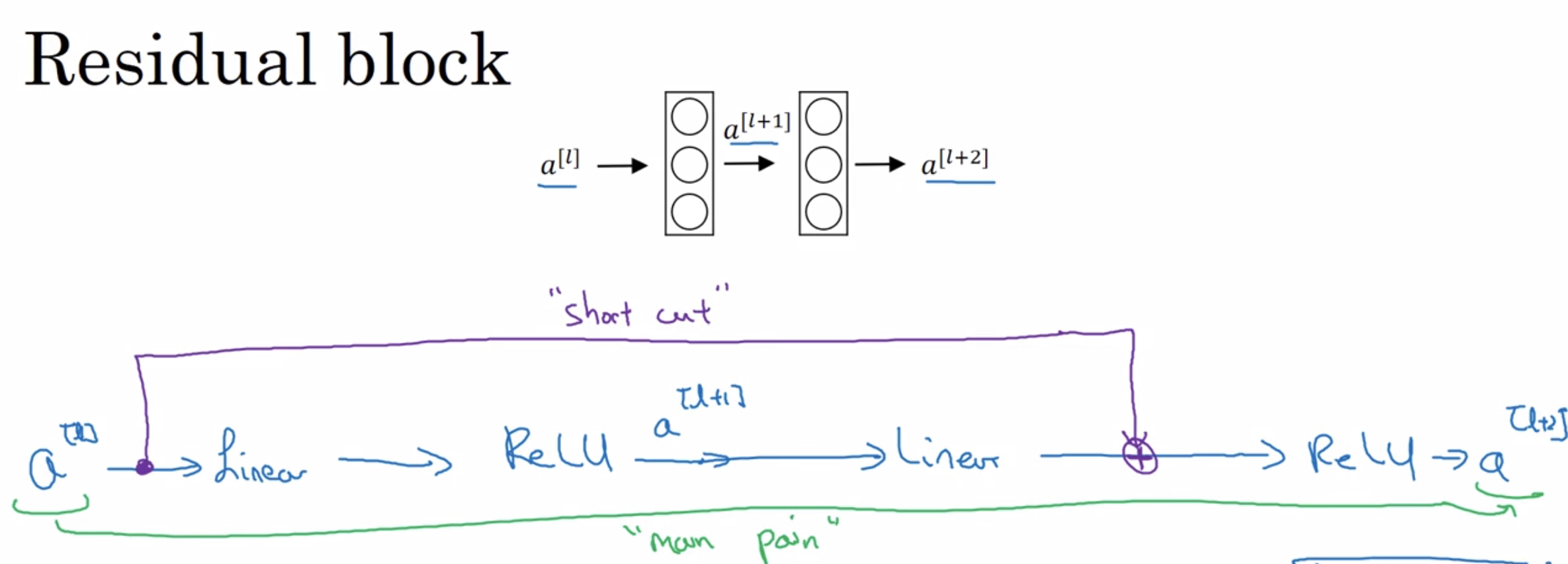
残差块是在一个深层的网络内，将前层与比较深的后层建立联系。上图以一个双线性层举例，从最上面的结构变成了下面的结构。

从公式上来说，线性层的公式为： $$ z^{[l+1]}=W^{[l+1]}a^{[l]}+b^{[l+1]}\ a^{[l+1]}=g(z^{[l+1]})\ z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]}\ a^{[l+2]}=g(z^{[l+2]}) $$ 而残差块则是将最后一个激活函数给修改了，也就是修改了上面的最后一个公式： $$ a^{[l+2]}=g(z^{[l+2]}+a^{[l]}) $$ 相当于加上了一个前层的激活值进行新的激活，这被称为是一个short cut，如果这种连接跨越了很多层，你可能还能听到一个术语叫skip connection，中文意思叫远跳连接。

我使用深度神经网络进行训练的时候会发现，随着网络深度的提升，训练的错误率会先下降后上升。而残差网络的出现，解决了这一问题，即使100层的网络也不会出现错误率提升的现象。这使得我们在训练深度网络的时候，解决了梯度消失和梯度爆炸的问题。

那么为什么残差网络的做法能够达到这样的效果呢？

$$ a^{[l+2]}=g(z^{[l+2]}+a^{[l]})=a(W^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]})\ 假设当到l+2层时，W^{[l+2]}和b^{[l+2]}都变成0，a^{[l+2]}=a^{[l]}\ 相当于在该层时出现了梯度消失/梯度爆炸,那么此时残差网络，就可以使网络停止在出现该问题之间。 $$

如果$l$层和$l+2$层的维度不同，则需要对公式做一个变形： $$ a^{[l+2]}=g(z^{[l+2]}+W_sa^{[l]})\ W_s使用来转换维度的，padding用0来填充。 $$

网络中的网络 & $1\times 1$卷积

对于单通道的图片，1$\times$1卷积没什么用。假设你有一张多通道的图片，比如32通道，使用一个1$\times$1$\times$32的卷积核进行卷积，然后应用ReLU激活函数。这样设计的原因和在卷积的每个通道上相当于设计了一个全连接层。

1$\times$1网络的应用场景如下：假设你需要将一个$28\times28\times192$的图片转化成为$28\times28\times32$的图片，在通常情况下，需要使用padding=same的32个192通道的卷积核实现，但因为padding是有损的。这时候$1\times1\times192$的卷积核就派上用场了。

谷歌Inception网络介绍

GoogLeNet是2014年Christian Szegedy提出的一种全新的深度学习结构，在这之前的AlexNet、VGG等结构都是通过增大网络的深度（层数）来获得更好的训练效果，但层数的增加会带来很多负作用，比如overfit、梯度消失、梯度爆炸等。inception的提出则从另一种角度来提升训练结果：能更高效的利用计算资源，在相同的计算量下能提取到更多的特征，从而提升训练结果。

inception结构示例如下所示：

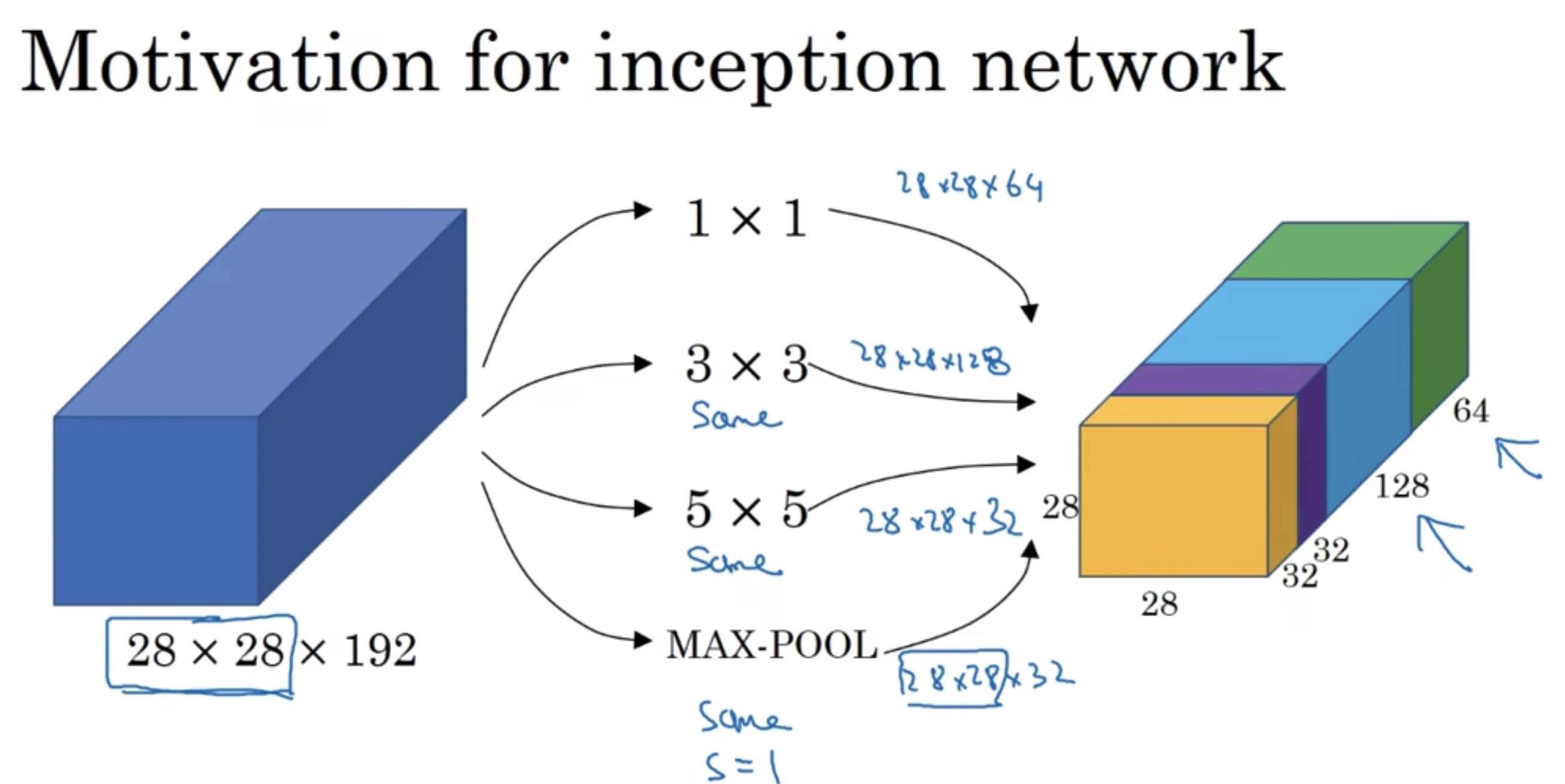
首先我们先来举个例子看一下，1$\times$1的卷积网络可以打打降低成本。

假设一个$28\times28\times192$的网络直接通过32个$5\times5$的卷积核进行padding=same的变化，计算成本为$28\times28\times32\times5\times5\times192=1.2$亿次乘法运算。

如果我们在中间加若干个$1\times1\times192$的卷积核做过渡，假设加了16个卷积核，那么计算成本则变为$28\times28\times16\times192+28\times28\times32\times5\times5\times16=1240$万次乘法运算，大约缩减到了$\frac{1}{10}$。

如果对inceotion中的每一个网络都做$1\times1$的卷积，那么上图中的结构变化成如下结构：

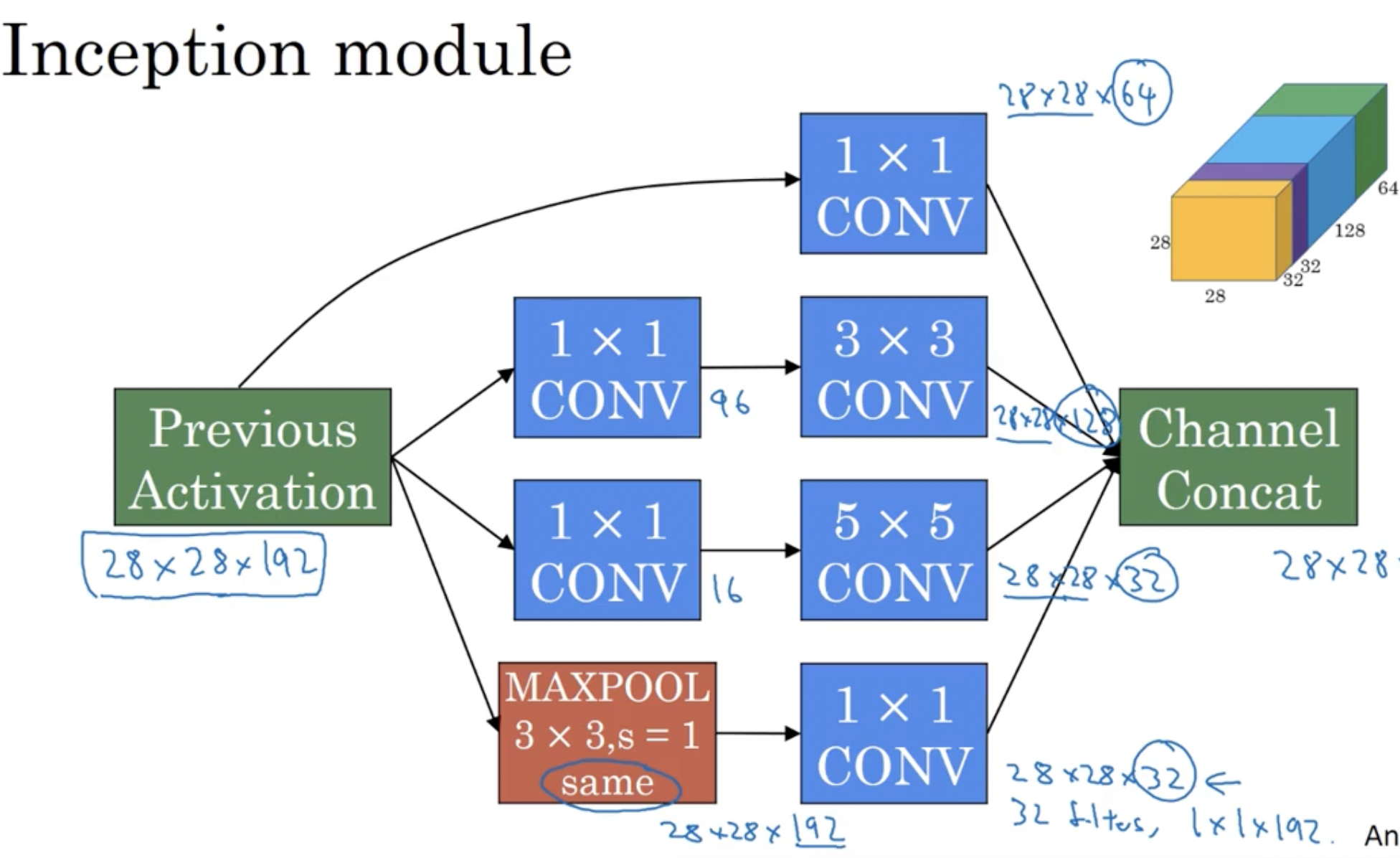
这就是一个完整的inception模块。

迁移学习

我们如何使用别人训练好的权重参数运用到自己的网络中呢？

以ImageNet数据集的网络为例，因为它是一个1000分类的问题，如何运用到我们自己的4分类问题上呢？最好的办法就是将原有的softmax层去掉，设计自己的softmax层。还有就是训练的过程中，那些预先训练好的参数是不参与你后续的训练的：这有两种实现方式，第一种就是通过框架来调整参数，使得前面的参数不参与前向和后向传播；第二种方式就是将x输入，在训练好的参数的计算下，保存输出的结果，用于后续自己的训练。

但如果你的数据集是一个很小的数据集，该如何做呢？

那么我们可能需要只冻结预训练网络的前层网络，构建自己的输出单元，训练后层网络。或者你可以将后层的网络换成自己的网络。

那么如果你的数据集比较大，如何做呢？

我们不需要冻结任何的网络，直接将预训练好的网络当做初始化，修改输出单元，直接进行训练。

数据增强

数据增强的方式如下：

• 垂直镜像对称
• 随机裁剪
• 局部扭曲
• 色彩转化： 会使你的模型对颜色更具鲁棒性。

因为有部分公式可能因为博客插件不支持的原因，完整的笔记请看: https://github.com/caixiongjiang/deep-learning-computer-vision

最后修改于 2022-08-01